No CrossRef data available.
Published online by Cambridge University Press: 18 April 2024
Let 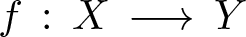 $f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism between irreducible smooth projective curves over an algebraically closed field of arbitrary characteristic. We prove that the vector bundle
$f\,:\,X\,\longrightarrow \,Y$ be a generically smooth morphism between irreducible smooth projective curves over an algebraically closed field of arbitrary characteristic. We prove that the vector bundle 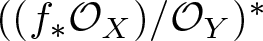 $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated. Moreover,
$((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is virtually globally generated. Moreover, 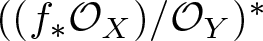 $((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample if and only if f is genuinely ramified.
$((f_*{\mathcal O}_X)/{\mathcal O}_Y)^*$ is ample if and only if f is genuinely ramified.