Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T12:39:20.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudo-umbilical surfaces with constant Gauss curvature

Published online by Cambridge University Press:  20 January 2009

Bang-Yen Chen
Bang-Yen Chen
Affiliation:
Michigan State University, East Lansing, Michigan 48823
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let M be a surface immersed in an m-dimensional space form Rm(c) of curvature c = 1, 0 or −1. Let h be the second fundamental form of this immersion; it is a certain symmetric bilinear mapping for x ∈ M, where Tx is the tangent space and 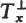the normal space of M at x. Let H be the mean curvature vector of M in Rm(c) and 〈, 〉 the scalar product on Rm(c). If there exists a function λ on M such that 〈h(X, Y), H〉 = λ〈X, Y〉 for all tangent vectors X, Y, then M is called a pseudo-umbilical surface of Rm(c). Let D denote the covariant differentiation of Rm(c) and η be a normal vector field. If we denote by D*η the normal component of Dη, then D* defines a connection in the normal bundle. A normal vector field η is said to be parallel in the normal bundle if Dη = 0. The length of mean curvature vector is called the mean curvature.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 18 , Issue 2 , December 1972 , pp. 143 - 148
Copyright
Copyright © Edinburgh Mathematical Society 1972

References

REFERENCES

(1) Chen, B.-Y., Minimal surfaces of Sm with Gauss curvature≦ 0, Proc. Amer. Math. Soc. 31 (1972), 235–238.Google Scholar
(2) Chen, B.-Y., Pseudo-umbilical submanifolds of a Riemannian manifold of constant curvature, III, J. Differential Geometry (to appear).Google Scholar
(3) Chen, B.-Y. and Ludden, G. D., Rigidity theorems for surfaces in euclidean space, Bull. Amer. Math. Soc. 78 (1972), 72–73.CrossRefGoogle Scholar
(4) Chern, S. S., Carmo, M. Do and Kobayashi, S., Minimal submanifolds of a sphere with second fundamental form of constant length, Functional Analysis and Related Fields (Springer-Verlag, 1970), 60–75.Google Scholar
(5) Lawson, H. B., Local rigidity theorems for minimal hypersurfaces, Ann. of Math. (2) 89 (1969), 187–197.CrossRefGoogle Scholar