Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T06:50:59.599Z Has data issue: false hasContentIssue false
  • English
  • Français

A Problem in Partitions: Enumeration of Elements of a given Degree in the free commutative entropic cyclic Groupoid

Published online by Cambridge University Press:  20 January 2009

H. Minc
H. Minc
Affiliation:
The University of British Columbia, Vancouver, Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A groupoid is a set closed with respect to a binary operation. It is commutative and entropic if xy = yx and xy.zw = xz.yw hold for all its elements. It is cyclic if it is generated by one element. Let x be the generator of the free commutative entropic cyclic groupoid 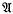. Then any element of 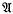can be written in the form xP where x1 = x and xQ+R = xQxR. Two indices P, Q are equal (called “concordant” in (3)) if and only if xP = xQ. The groupoid of these indices, the free additive commutative entropic logarithmetic (cf. (3)), is clearly isomorphic to .

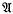Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 11 , Issue 4 , November 1959 , pp. 223 - 224
Copyright
Copyright © Edinburgh Mathematical Society 1959

References

REFERENCES

Etherington, I. M. H., On non-associative combinations, Proc. Roy. Soc. Edin., 59 (1939), 153–162.CrossRefGoogle Scholar
Mine, H., Index polynomials and bifurcating root-trees, Proc. Roy. Soc. Edin., A, 64 (1957), 319–341.Google Scholar
Mine, H., The free commutative entropic logarithmetic, Proc. Roy. Soc. Edin., A, 65 (1959), 177–192.Google Scholar
Mine, H., Enumeration of indices of given altitude and potency, Proc. Edin. Math. Soc. 11 (1959), 207–209.Google Scholar