Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-27T22:49:20.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial algebras over the Steenrod algebra variations on a theorem of Adams and Wilkerson

Published online by Cambridge University Press:  20 January 2009

Larry Smith  and
R. M. Switzer
Larry Smith
Affiliation:
Mathematisches InstitutBunsenstrasse 3/5D3400 GÖttingen, FED. REP. OF GERMANY
R. M. Switzer
Affiliation:
Mathematisches InstitutBunsenstrasse 3/5D3400 GÖttingen, FED. REP. OF GERMANY
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The problem of deciding which graded polynomial algebras over the field 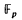of p elements can occur as the 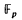-cohomology of a space has played a central rôle in the development of algebraic topology beginning as early as 1950. In the case where the polynomial generators do not occur in dimensions divisible by p, Adams and Wilkerson [1] have given a complete solution by showing that the spaces constructed by Clark and Ewing [3] suffice to realize all such algebras as 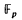-cohomology rings. The main result of Adams and Wilkerson for odd primes can be stated as follows.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 1 , February 1984 , pp. 11 - 19
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

REFERENCES

1.Adams, J. F. and Wilkerson, C. W., Finite H-spaces and algebras over the Steenrod algebra, Ann. of Math. 111 (1980), 95–143.CrossRefGoogle Scholar
2.Clark, A., On π3 of finite dimensional H-spaces, Ann. of Math. 78 (1963), 193–195.CrossRefGoogle Scholar
3.Clark, A. and Ewing, J., The realization of polynomial algebras as cohomology rings, Pacific J. Math. 50 (1974), 425–434.CrossRefGoogle Scholar
4.Lang, S., Algebra (Addison-Wesley, 1965).Google Scholar
5.Serre, J. -P., Sur la dimension cohomologique des groupes profini, Topology 3 (1965), 413–420.CrossRefGoogle Scholar
6.Shephard, G. C. and Todd, J. A., Finite unitary reflection groups, Canadian J. Math. 6 (1954), 274–304.Google Scholar
7.Smith, L. and Switzer, R. M., Readability and nonrealizability of Dickson algebras as cohomology rings, preprint.Google Scholar
8.Wilkerson, C. W., Classifying spaces, Steenrod operations and algebraic closure, Topology 16 (1977), 227–237.CrossRefGoogle Scholar
9.Wilkerson, C. W., Integral closure of unstable Steenrod algebra actions, J. Pure and Appl. Alg. 13 (1978), 49–55.CrossRefGoogle Scholar