Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T01:12:12.387Z Has data issue: false hasContentIssue false
  • English
  • Français

A Pair of Dual Integral Equations Involving Bessel Functions of the First and the Second Kind

Published online by Cambridge University Press:  20 January 2009

R. P. Srivastav
R. P. Srivastav
Affiliation:
Department of Mathematics, Indian Institute of Technology, Kanpur, (U.P.), India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give a method for the solution of the dual integral equations

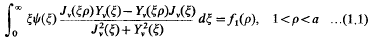
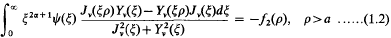
where Jv and Yv are Bessel functions of the first and second kind, −½≦α≦½, f1(ρ) and f2(ρ) are known functions and ψ(ξ) is to be determined. Such equations arise in the discussion of boundary value problems for half-spaces containing a cylindrical cavity. For example, let us take the problem of finding a potential function φ(ρ, θ, z) which satisfies Laplace's equation for

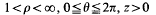
subject to the usual regularity conditions and the following boundary conditions:

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 14 , Issue 2 , December 1964 , pp. 149 - 158
Copyright
Copyright © Edinburgh Mathematical Society 1964

References

REFERENCES

(1)Weber, H., Über die Besselschen Funktionen und ihre Anwendung an die Theorie der Elektrischen Ströme, J. f. Math., 75 (1873), 75.Google Scholar
(2)Beltrami, E., Sulla teoria della funzioni potenziali simmetriche, Rend. Acc. d. Sci. di Bologna (1881), 461.Google Scholar
(3)Titchmarsh, E. C., Introduction to the Theory of Fourier Integrals (Oxford, 1937), p. 334.Google Scholar
(4)Busbridge, I. W., Dual integral equations, Proc. London Math. Soc., 44 (1938), 115.CrossRefGoogle Scholar
(5)Gordon, A. N., Dual integral equations, J. London Math. Soc., 29 (1954), 360.CrossRefGoogle Scholar
(6)Sneddon, I. N., The elementary solution of dual integral equations, Proc. Glasgow Math. Assoc., 4 (1960), 108.CrossRefGoogle Scholar
(7)Copson, E. T., On certain dual integral equations, Proc. Glasgow Math. Assoc., 5 (1961), 21.CrossRefGoogle Scholar
(8)Noble, B., On some dual integral equations, Quart. J. Math. (2), 6 (1955), 81.CrossRefGoogle Scholar
(9)Tranter, C. J., On some dual integral equations, Quart. J. Math. (2), 2 (1951), 60.CrossRefGoogle Scholar
(10)Williams, W. E., The solution of certain dual integral equations, Proc. Edinburgh Math. Soc., 12 (1961), 213.CrossRefGoogle Scholar
(11)Erdelyi, A. and Sneddon, I. N., Fractional integration and dual integral equations, Canadian J. Math., 14 (1962), 685.CrossRefGoogle Scholar
(12)Lowengrub, M. and Sneddon, I. N., The solution of a pair of dual integral equations, Proc. Glasgow Math. Assoc., 6 (1963), 14.CrossRefGoogle Scholar
(13)Williams, W. E., Dual integral equations, Proc. Glasgow Math. Assoc. (to appear).Google Scholar
(14)Cooke, J. C. and Tranter, C. J., Dual Fourier-Bessel series, Quart. J. Mech. Appl. Math., 12 (1959), 379.CrossRefGoogle Scholar
(15)Sneddon, I. N. and Srivastav, R. P., Dual Series Relations—I, Dual relations involving Fourier-Bessel series, Proc. Roy. Soc. Edinburgh, Series A, 66 (1962–1963), 150–160.Google Scholar
(16)Srivastav, R. P., An axisymmetric mixed boundary value problem for a half-space with a cylindrical cavity, J. Math. Mech. 13 (1964), 385.Google Scholar
(17)Tranter, C. J., On some dual integral equations occurring in potential problems with axial symmetry, Quart. J. Mech. and Appl. Math., 3 (1950), 411.CrossRefGoogle Scholar
(17a)Tranter, C. J., A further note on dual integral equations and an application to the diffraction of electromagnetic waves, Quart. J. Mech. and Appl. Math., 7 (1954), 318.CrossRefGoogle Scholar
(18)Cooke, J. C., A solution of Tranter's dual integral equations problem, Quart. J. Mech. and Appl. Math., 9 (1956), 103.CrossRefGoogle Scholar
(19)Noble, B., Certain dual integral equations, J. Math. Phys., 37 (1958), 128.CrossRefGoogle Scholar
(20)Watson, G. N., A Treatise on the Theory of Bessel Functions (Cambridge University Press, 1944).Google Scholar
(21)Erdélyi, A. et al. , Tables of Integral Transforms, Vol. 2 (McGraw Hill, 1954).Google Scholar
(22)Titchmarsh, E. C., Eigenfunction Expansions associated with Second-order differential equations (Oxford, 1946).Google Scholar