Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T19:39:42.381Z Has data issue: false hasContentIssue false
  • English
  • Français

The Operator Space Projective Tensor Product: Embedding into the Second Dual and Ideal Structure

Published online by Cambridge University Press:  05 September 2013

Ranjana Jain  and
Ajay Kumar
Ranjana Jain
Affiliation:
Department off Mathematics, Lady Shri Ram College for Women, Lajpat Nagar IV, New Delhi 110024, India, ([email protected])
Ajay Kumar
Affiliation:
Department of Mathematics, University of Delhi, Delhi 110007, India, ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that, for operator spaces V and W, the operator space V** ⊗hW** can be completely isometrically embedded into (V ⊗hW)**, ⊗h being the Haagerup tensor product. We also show that, for exact operator spaces V and W, a jointly completely bounded bilinear form on V × W can be extended uniquely to a separately w*-continuous jointly completely bounded bilinear form on V× W**. This paves the way to obtaining a canonical embedding of 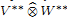into 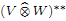with a continuous inverse, where 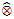is the operator space projective tensor product. Further, for C*-algebras A and B, we study the (closed) ideal structure of 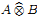which, in particular, determines the lattice of closed ideals of 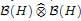completely.

Keywords

operator spaceC*-algebrasoperator space projective normHaagerup normPrimary 46L0646L0747L25
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 57 , Issue 2 , June 2014 , pp. 505 - 519
Copyright
Copyright © Edinburgh Mathematical Society 2014 

References

1.Allen, S. D., Sinclair, A. M. and Smith, R. R., The ideal structure of the Haagerup tensor product of C*-algebras, J. Reine Angew. Math. 442 (1993), 111–148.Google Scholar
2.Archbold, R. J., Kaniuth, E., Schlichting, G. and Somerset, D. W. B., Ideal spaces of the Haagerup tensor product of C*-algebras, Int. J. Math. 8 (1997), 1–29.Google Scholar
3.Blackadar, B., Operator algebras: theory of C*-algebras and von-Neumann algebras (Springer, 2006).CrossRefGoogle Scholar
4.Blecher, D. P. and Lemerdy, C., Operator algebras and their modules: an operator space approach, London Mathematical Soceity Monographs, New Series, Volume 30 (Clarendon Press, Oxford University Press, Oxford, 2004).Google Scholar
5.Blecher, D. P. and Paulsen, V. I., Tensor product of operator spaces, J. Funct. Analysis 99 (1991), 262–292.CrossRefGoogle Scholar
6.Cohen, P. J., Factorization in group algebras, Duke Math. J. 26 (1959), 199–205.CrossRefGoogle Scholar
7.Dixon, P. G., Non-closed sums of closed ideals in Banach algebras, Proc. Am. Math. Soc. 128 (2000), 3647–3654.Google Scholar
8.Effros, E. G. and Ruan, Z.-J., On approximation properties for operator spaces, Int. J. Math. 19 (1990), 163–187.Google Scholar
9.Effros, E. G. and Ruan, Z.-J., A new approach to operator spaces, Can. Math. Bull. 34 (1991), 329–337.Google Scholar
10.Effros, E. G. and Ruan, Z.-J., Operator spaces, London Mathematical Society Monographs, New Series, Volume 23 (Clarendon Press, Oxford University Press, New York, 2000).Google Scholar
11.Graham, C. C. and McGehee, O. C., Essays in commutative harmonic analysis (Springer, 1979).CrossRefGoogle Scholar
12.Haagerup, U., The Grothendieck inequality for bilinear forms on C*-algebras, Adv. Math. 56 (1985), 93–116.Google Scholar
13.Haagerup, U. and Musat, M., The Effros–Ruan conjecture for bilinear forms on C*-algebras, Invent. Math. 174 (2008), 139–163.Google Scholar
14.Jain, R. and Kumar, A., Operator space tensor products of C*-algebras, Math. Z. 260 (2008), 805–811.Google Scholar
15.Kaniuth, E., A course in commutative Banach algebras (Springer, 2009).Google Scholar
16.Kumar, A., Operator space projective tensor product of C*-algebras, Math. Z. 237 (2001), 211–217.Google Scholar
17.Kumar, A., Involution and the Haagerup tensor product, Proc. Edinb. Math. Soc. 44 (2001), 317–322.Google Scholar
18.Kumar, A. and Sinclair, A. M., Equivalence of norms on operator space tensor products of C*-algebras, Trans. Am. Math. Soc. 350 (1998), 2033–2048.Google Scholar
19.Pisier, G. and Shlyakhtenko, D., Grothendieck's theorem for operator spaces, Invent. Math. 150 (2002), 185–217.Google Scholar
20.Rudin, W., Functional analysis, 2nd edn (McGraw-Hill, 1991).Google Scholar
21.Sanchez, F. C. and Garcia, R., The bidual of a tensor product of Banach spaces, Rev. Mat. Ibero. 21 (2005), 843–861.CrossRefGoogle Scholar
22.Smith, R. R., Completely bounded module maps and the Haagerup tensor product, J. Funct. Analysis 102 (1991), 156–175.Google Scholar
23.Takesaki, M., Theory of operator algebras, I (Springer, 1979).Google Scholar
24.Wassermann, S., A pathology in the ideal space of L(H) ⊗ L(H), Indiana Univ. Math. J. 27 (1978), 1011–1020.CrossRefGoogle Scholar