Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Erlacher, Evelina
and
Grosser, Michael
2013.
Pseudo-Differential Operators, Generalized Functions and Asymptotics.
p.
253.
Kastis, E.
and
Power, S.C.
2015.
The operator algebra generated by the translation, dilation and multiplication semigroups.
Journal of Functional Analysis,
Vol. 269,
Issue. 10,
p.
3316.
Kastis, E.
2017.
The parabolic algebra on L spaces.
Journal of Mathematical Analysis and Applications,
Vol. 455,
Issue. 1,
p.
698.
Kastis, Eleftherios
2019.
The norm closed triple semigroup algebra.
Israel Journal of Mathematics,
Vol. 230,
Issue. 2,
p.
855.


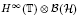 .
.