Hostname: page-component-55f67697df-4ks9w Total loading time: 0 Render date: 2025-05-10T01:41:41.558Z Has data issue: false hasContentIssue false
  • English
  • Français

On traces of Bochner representable operators on the space of bounded measurable functions

Part of: Special classes of linear operators Linear function spaces and their duals Measures, integration, derivative, holomorphy

Published online by Cambridge University Press:  11 January 2024

Marian Nowak Open the ORCID record for Marian Nowak [Opens in a new window]  and
Juliusz Stochmal Open the ORCID record for Juliusz Stochmal [Opens in a new window]
Marian Nowak
Affiliation:
Institute of Mathematics, University of Zielona Góra, ul. Szafrana 4A, 65-516 Zielona Góra, Poland ([email protected])
Juliusz Stochmal
Affiliation:
Institute of Mathematics, Kazimierz Wielki University, ul. Powstańców Wielkopolskich 2, 85-090 Bydgoszcz, Poland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Σ be a σ-algebra of subsets of a set Ω and 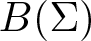$B(\Sigma)$ be the Banach space of all bounded Σ-measurable scalar functions on Ω. Let 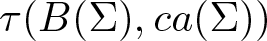$\tau(B(\Sigma),ca(\Sigma))$ denote the natural Mackey topology on 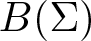$B(\Sigma)$. It is shown that a linear operator T from 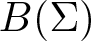$B(\Sigma)$ to a Banach space E is Bochner representable if and only if T is a nuclear operator between the locally convex space 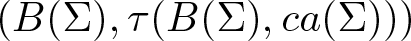$(B(\Sigma),\tau(B(\Sigma),ca(\Sigma)))$ and the Banach space E. We derive a formula for the trace of a Bochner representable operator 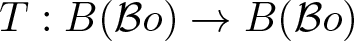$T:B({\cal B} o)\rightarrow B({\cal B} o)$ generated by a function 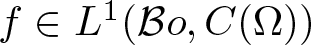$f\in L^1({\cal B} o, C(\Omega))$, where Ω is a compact Hausdorff space.

Keywords

Bochner representable operatorskernel operatorsnuclear operatorsspaces of bounded measurable functionstrace of operatorvector measures

MSC classification

Primary: 46G10: Vector-valued measures and integration 47B10: Operators belonging to operator ideals (nuclear, $p$-summing, in the Schatten-von Neumann classes, etc.) 46E27: Spaces of measures
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 1 , February 2024 , pp. 224 - 235
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aliprantis, C. D., and Burkinshaw, O., Locally Solid Riesz Spaces with Applications to Economics, Math. Surveys and Monographs, Vol. 105 (AMS, Providence, RI, 2003).CrossRefGoogle Scholar
Brislawn, C., Kernels of trace class operators, Proc. Amer. Math. Soc. 104(4): (1988), 1181–1190.CrossRefGoogle Scholar
Conway, J. B., A Course in Functional Analysis, 2nd ed., (Springer-Verlag, New York, 1990).Google Scholar
Delgado, J., A trace formula for nuclear operators on Lp, in Pseudo-Differential Operators: Complex Analysis and Partial Differential Equations, Operator Theory: Advances and Applications, Vol. 205 (Birkhäuser, Basel, 2009), .Google Scholar
Diestel, J., The Radon-Nikodym property and the coincidence of integral and nuclear operators, Rev. Roumaine Math. Pures Appl. 17 (1972), 1611–1620.Google Scholar
Diestel, J., Applications of weak compactness and bases to vector measures and vectorial integration, Rev. Roumaine Math. Pures Appl. 18 (1973), 211–224.Google Scholar
Diestel, J., and Uhl, J. J., Vector Measures, Math. Surveys, Vol. 15 (American Mathematical Society, Providence, RI, 1977).CrossRefGoogle Scholar
Dinculeanu, N., Vector Integration and Stochastic Integration in Banach Spaces, (Wiley-Interscience, New York, 2000).CrossRefGoogle Scholar
Drewnowski, L., Topological rings of sets, continuous set functions, integration, III, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astron. Phys. 20 (1972), 439–445.Google Scholar
Gohberg, I., Goldberg, S. and Krupnik, N., Traces and Determinants of Linear Operators (Springer, Basel, 2000).CrossRefGoogle Scholar
Graves, W. H. and Ruess, W., Compactness in spaces of vector-valued measures and a natural Mackey topology for spaces of bounded measurable functions, Contemp. Math. 2 (1980), 189–203.CrossRefGoogle Scholar
Grothendieck, A., Sur les espaces (F) et (DF), Summa Brasil. Math. 3 (1954), 57–123.Google Scholar
Grothendieck, A., Produits tensoriels topologiques et espaces nucléaires, Mem. Amer. Soc. 16 (1955), .Google Scholar
Grothendieck, A., La théorie de Fredholm, Bull. Soc. Math. France 84 (1956), 319–384.CrossRefGoogle Scholar
Jarchow, H., Locally Convex Spaces (Teubner, Stuttgart, 1981).CrossRefGoogle Scholar
Khurana, S. S., A topology associated with vector measures, J. Indian Math. Soc. 45 (1981), 167–179.Google Scholar
Nowak, M., Vector measures and Mackey topologies, Indag. Math. 23(1–2) (2012), 113–122.CrossRefGoogle Scholar
Nowak, M., Mackey topologies and compactness in spaces of vector measures, Funct. Approx. 50(1) (2014), 191–198.Google Scholar
Nowak, M., Nuclear operators and applications to kernel operators, Math. Nachr. 296(5) (2023), 2109–2120.CrossRefGoogle Scholar
Nowak, M., Topological properties of complex lattice of bounded measurable functions, J. Function Spaces and Appl. 2013 (2013), .Google Scholar
Pietsch, A., Nuclear Locally Convex Spaces, Ergebnisse der Mathematik und Ihrer Grenzebiete, Vol. 66 (Springer-Verlag, Berlin, Heidelberg, New York, 1972).Google Scholar
Pietsch, A., Eigenvalues and s-Numbers (Akadem. Verlagsges. Geest & Portig, Leipzig, 1987).Google Scholar
Ryan, R., Introduction to Tensor Products of Banach Spaces, Springer Monographs in Mathematics (Springer, London, 2002).CrossRefGoogle Scholar
Schaefer, H. H., Topological Vector Spaces (Springer-Verlag, New York, Heidelberg, Berlin, 1971).CrossRefGoogle Scholar
Sofi, M. A., Vector measures and nuclear operators, Illin. J. Math. 49(2): (2005), 369–383.Google Scholar
Tong, A. E., Nuclear mappings on C(X), Math. Ann. 194 (1971), 213–224.CrossRefGoogle Scholar
Trèves, F., Topological Vector Spaces, Distributions and Kernels, (Dover Publications, New York, 1967).Google Scholar
Yosida, K., Functional Analysis, 4th Ed., (Springer-Verlag, Berlin, Heidelberg, New York, 1974).CrossRefGoogle Scholar