In (1) I obtained † an asymptotic formula for the number of zeros of an arbitrary canonical product II(z) of integral order but not of mean type, all of whose zeros lie on a single radius, from a knowledge of the asymptotic behaviour of (i)log | П(z)| as | z | = r→ ∞ along another radius l, with certain side conditions. After proving the analogous theorem in which log | П(z)| in (i) is replaced by 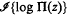, I show in this note that, at a cost of replacing l by two radii l1 and l2, both of these theorems may be generalised to include a class of canonical products of integral order whose zeros lie along a whole line. In one of the resulting theorems ‡ (Theorem II) I find the asymptotic number of zeros on each half of the line of zeros; another theorem (Theorem III) includes a previous result of mine.§