Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-01T00:04:03.306Z Has data issue: false hasContentIssue false
  • English
  • Français

On the strong radical of certain Banach algebras

Published online by Cambridge University Press:  20 January 2009

Bertram Yood
Bertram Yood
Affiliation:
Pennsylvania State University, University Park, PA. 16802, U.S.A..
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a complex Banach algebra. By an ideal in A we mean a two-sided idealunless otherwise specified. As in (7, p. 59) by the strong radical 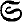of A we mean theintersection of the modular maximal ideals of A (if there are no such ideals we set 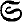=A). Our aim is to discuss the nature of 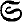and the relation of 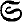to A for a specialclass of Banach algebras. Henceforth A will denote a semi-simple modular annihilatorBanach algebra (one for which the left (right) annihilator of each modular maximalright (left) ideal is not (0)). For the theory of such algebras see (2) and (9).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 21 , Issue 1 , March 1978 , pp. 81 - 85
Copyright
Copyright © Edinburgh Mathematical Society 1978

References

REFERENCES

(1) Alexander, F. E.,Some counter-examples of annihilator, dual and complemented A*-algebras, J. London Math. Soc. (2) 8 (1974), 735–740.CrossRefGoogle Scholar
(2) Barnes, B. A., Modular annihilator algebras, Canad. J. Math. 18 (1966), 566–578.CrossRefGoogle Scholar
(3) Barnes, B. A., Banach algebras which are ideals in a Banach algebra, Pacific J.Math. 38(1971), 1–7.CrossRefGoogle Scholar
(4) Bonsall, F. F. and Duncan, J., Complete Normed Algebras (Springer-Verlag, 1973).CrossRefGoogle Scholar
(5) Bonsall, F. F. and Goldie, A. W., Annihilator algebras, Proc. London Math. Soc. (3) 4 (1954), 154–167.CrossRefGoogle Scholar
(6) Burnham, J. T., Closed ideals in subalgebras of Banach aigebras 1, Proc. Amer. Math. Soc. 32(1972), 551–555.CrossRefGoogle Scholar
(7) Rickart, C. E., General Theory of Banach Algebras (Van Nostrand, 1960).Google Scholar
(8) Tullo, A. W., Conditions on Banach algebras which imply finite-dimensionality, Proc. Edinburgh Math. Soc. 20 (1976), 1–5.CrossRefGoogle Scholar
(9) Yood, B., Ideals in topological rings, Canad. J. Math. 16 (1964), 28–45.CrossRefGoogle Scholar
(10) Yood, B., Closed prime ideals in topological rings, Proc. London Math. Soc. (3) 24 (1972), 307–323.CrossRefGoogle Scholar
(11) Garling, D. J. H., On ideals of operators in Hilbert space, Proc. London Math. Soc. (3) 17(1967), 115–138.CrossRefGoogle Scholar