No CrossRef data available.
Article contents
On the stationary eccentricity of a system of four-tangent conics
Published online by Cambridge University Press: 20 January 2009
Extract
Let the convex quadrilateral formed by the four given tangents be ABA′B′, and O the intersection of the diagonals. Let OA and OB be taken as axes of x and y. Denote OA, OA′, OB and OB′ by a, a′, b and b′, a and b being positive, and a′ and b′ negative. The tangential equation of the system is then
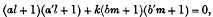
where k is a variable parameter; for the equation is satisfied when the straight line lx + my + 1 = 0 passes through any two adjacent angular points of the quadrilateral.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1909
References
page 3 note * The ellipses of the system are always real, for the equation referred to the centre as origin is ![]() . Hence the ellipses are real as long as B is negative. Now
. Hence the ellipses are real as long as B is negative. Now ![]() which is negative when k is within the elliptio limits.
which is negative when k is within the elliptio limits.


