Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:27:06.071Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Solution of Differential Equations by Definite Integrals

Published online by Cambridge University Press:  20 January 2009

E. T. Whittaker
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is well known that in many cases the solutions of a linear differential equation can be expressed as definite integrals, different solutions of the same equation being represented by integrals which have the same integrand, but different paths of integration. Thus, the various solutions of the hypergeometric differential equation

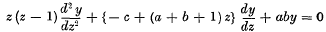
can be represented by integrals of the type

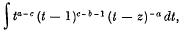
the path of integration being (for one particular solution) a closed circuit encircling the point t = 0 in the positive direction, then the point t = 1 in the positive direction, then the point t = 0 in the negative direction, and lastly the point t = 1 in the negative direction; or (for another particular solution) an arc in the t-plane joining the points t = 1 and t = ∞.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 2 , Issue 4 , June 1931 , pp. 189 - 204
Copyright
Copyright © Edinburgh Mathematical Society 1931

References

page 190 note 1 CfWhittcaker, , Analytical Dynamics, § 126.Google Scholar

page 192 note 1 CfForsyth, A. R., Treatise on Differential Equations, Chapter VII., “Solution by Definite Integrals.”Google Scholar

page 195 note 1 CfWhittaker, and Watson, , Modern Analysis, §14.5.Google Scholar

page 197 note 1 CfWhittaker, and Watson, , Modern Analysis, § 14.6.Google Scholar

page 198 note 1 Such integrals have been used in the solution of third-order equations by Schlesinger, L., Math. ZS., 27 (1928), p. 504.CrossRefGoogle Scholar

page 204 note 1 Riemann, , Berlin Monatsb., Nov. 1859 :Google ScholarMellin, , Acta Math., 25 (1902), p. 138 :Google ScholarMath. Ann., 68 (1909), p. 305.Google Scholar