Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T00:46:54.705Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Singular Points of Plane Curves

Published online by Cambridge University Press:  20 January 2009

T. B. Sprague
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the general equation of a curve that passes through the origin,

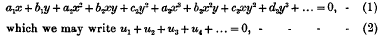
u1 ≡ a1x + b1y = 0 is the equation to the tangent at the origin; for, y q g when x and y are very small, we may neglect all the terms in comparison with those involving the first powers of x and y. If neither a1 nor b1 vanishes, we may, without loss of generality, write the equation in the form

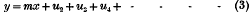
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 21 , February 1902 , pp. 96 - 110
Copyright
Copyright © Edinburgh Mathematical Society 1902

References

page 96 note * In all the figures the darker lines represent the evolute.