Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T01:00:15.766Z Has data issue: false hasContentIssue false
  • English
  • Français

On the relations between the numbers of standard tableaux

Published online by Cambridge University Press:  20 January 2009

D. E. Rutherford
D. E. Rutherford
Affiliation:
The University, St Andrews.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

§ 1. Corresponding to any partition

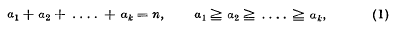
which we denote by [a1, . …, ak] or briefly by [a], of the integer n, we can construct a shape which has a1 spaces in the first row, a2 in the second row, . …, ak in the kth and last row. Thus the shape corresponding to the partition [5, 3, 3, 2] of 13 has the form:

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 7 , Issue 1 , October 1942 , pp. 51 - 54
Copyright
Copyright © Edinburgh Mathematical Society 1942

References

1 Proc. London Math. Soc., 33 (1901), 97; 34 (1902), 361; (2) 28 (1928), 255 ; (2) 31 (1930), 253 ; (2) 34 (1932), 196 ; (2) 37 (1934), 441; and other papers.Google Scholar