Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T13:58:38.071Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Relation between Inverse Factorial Series and Binomial Coefficient Series*

Published online by Cambridge University Press:  20 January 2009

W. L. Ferrar
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The chief aim of this note is to investigate directly the relation between the inverse factorial series

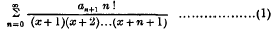
and the binomial coefficient series, or Newton's interpolation formula,

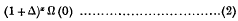
which may also represent Ω(x), the sum of the series (1).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 43 , February 1924 , pp. 92 - 102
Copyright
Copyright © Edinburgh Mathematical Society 1924

Footnotes

*

Added August 10th, 1925.—Science Progress for July 1925 notes a paper by J. Horn, “Math. Zeitschrift” 21 (1924) 85.95, in whioh work on differential and difference equations, previously done with inverse factorial series, is carried out with binomial coefficient series. I have been unable to consult the paper itself to see what points in the connection between the two types of series are exemplified.

References

† Further references to this paper will be given as Norlünd (1923).

* Acta Math. 37 (1914) 344. Further references to this are given as Norlünd (1914).

* Norlünd (1914), Theorem VII, 361.

† Norlünd (1923), 43.

* Pinchbrle, , Annales Sci. de l'Ecole Normale (3), 22 (1905), 50.Google Scholar

Bromwich, , loc. cit., p. 254, Ex. 1.Google Scholar

* By the test given by Hardy, . Proc. Lond. Math. Soc. (2), 4 (1907), 250–1.Google Scholar

† Whittaker, E. T., Proc. Royal Soc. Edinburgh, XXXV., (1915), 181–194.CrossRefGoogle Scholar