Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Díaz, Juan Carlos
and
Miñarro, M.Angeles
1993.
On Fréchet Montel spaces and their projective tensor product.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 113,
Issue. 2,
p.
335.
Defant, Andreas
and
Maestre, Manuel
1994.
Property (BB) and holomorphic functions on Fréchet-Montel spaces.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 2,
p.
305.
Boyd, C
and
Ryan, R.A
2001.
Geometric Theory of Spaces of Integral Polynomials and Symmetric Tensor Products.
Journal of Functional Analysis,
Vol. 179,
Issue. 1,
p.
18.


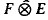 has the property (
has the property (