Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T00:07:30.375Z Has data issue: false hasContentIssue false
  • English
  • Français

On the projective geometry of paths

Published online by Cambridge University Press:  20 January 2009

J. Haantjes
J. Haantjes
Affiliation:
University of Edinburgh.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An affine connection in an n-dimensional manifold Xn defines a system of paths, but conversely a connection is not defined uniquely by a system of paths. It was shown by H. Weyl that any two affine connections whose components are related by an equation of the form

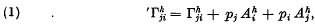
where 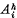is the unit affinor, give the same system of paths. In the geometry of a system of paths, a particular parameter on the paths, called the projective normal parameter, plays an important part. This parameter, which is invariant under a transformation of connection (1), was introduced by J. H. .C. Whitehead. It can be defined by means of a Schwarzian differential equation and it is determined up to linear fractional transformations. In § 1 this method is briefly discussed.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 5 , Issue 2 , June 1937 , pp. 103 - 115
Copyright
Copyright © Edinburgh Mathematical Society 1937

References

page 103 note 1 Weyl, H., “Zur Infinitesimalgeometrie: Einordnung der projektiven und der konformen Auffassung,” Göttinger Nachrichten (1921), pp. 99–112.Google Scholar

page 103 note In this paper the term “affinor” is used instead of “tensor.”

page 103 note 3 Whitehead, J. H. C., “The representation of projective spaces,” Ann. of Math., 32 (1931), pp. 327–360.CrossRefGoogle Scholar

page 103 note 4 Berwald, L., “On the projective geometry of paths,” Ann. of Math., 37 (1936), pp. 879–898.CrossRefGoogle Scholar

page 103 note 5 Dantzig, D. van, “Theorie des projektiven Zusammenhangs n-dimensionaler Räume,” Math. Annalen 106 (1932), pp. 400–454.CrossRefGoogle Scholar See also Schouten, J. A. and Haantjes, J., “Zur allgemeinen projektiven Differentialgeometrie,” Compositio Math. 3 (1935), pp. 1–51. This paper is referred to as A. P. D.Google Scholar

page 104 note 1 Weyl, H., l. c.Google Scholar

page 105 note 1 Thomas, T. Y., “On the projective and equiprojective geometry of paths,” Proc. Nat. Acad. Sci., U.S.A. 11 (1925), pp. 199–203;CrossRefGoogle Scholar “A projective theory of affinely connected manifolds,” Math. Zeitschrift 25 (1926), pp. 723–733.CrossRefGoogle Scholar

page 106 note 1 Whitehead, J. H. C., l. c.;Google ScholarBerwald, L., l. c., p. 882.Google Scholar

page 106 note 2 Whitehead, J. H. C., l. c., p. 338;Google ScholarBerwald, L., l. c., p. 884.Google Scholar

page 106 note 3 van Dantzig, D., l. c.Google Scholar

page 108 note 1 A. P. D., p. 32.Google Scholar

page 108 note 2 A. P. D., p. 33.Google Scholar

page 109 note 1 The equations are obtainable in this form by putting t = u 1/u o in x x = x x (t) and multiplying by an arbitrary homogeneous function of degree 1.

page 111 note 1 The sign means that the equation holds with respect to the coordinate system or systems used in the. equation itself; it need not hold with respect to another system.

page 112 note 1 A. P. D., p. 11.Google Scholar