If L, M, N denote Prof. Study's Dual Coordinates of a straight line (see Proc. Edinburgh Math. Soc., 44 (1926), 90–97), any (homogeneous) equation F (L, M, N) = 0 must define a certain system of lines. By the nature of dual numbers we must have

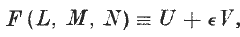
where U and V are functions of l, m, n, λ, μ, ν, the ordinary (Pluckerian) coordinates. Since F = 0 implies U = 0 and V = 0 the system of lines is a congruence. But it is a congruence of a very special kind, whose nature will now be considered.