Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T18:07:38.205Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Fatou theorem for ∂̄J-subsolutions in wedges

Part of: Holomorphic mappings and correspondences Global differential geometry

Published online by Cambridge University Press:  17 August 2022

Alexandre Sukhov
Alexandre Sukhov*
Affiliation:
Departement de Mathématique, University of Lille, Laboratoire Paul Painlevé, Villeneuve d'Ascq, Cedex 59655, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a version of the Fatou theorem for bounded functions with a bounded $\overline \partial _J$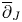 part of the differential on wedge-type domains in an almost complex manifold.

Keywords

almost complex manifold∂̄-operatorpseudoholomorphic discwedge-type domaintotally real manifoldthe Fatou theorem

MSC classification

Primary: 32H02: Holomorphic mappings, (holomorphic) embeddings and related questions 53C15: General geometric structures on manifolds (almost complex, almost product structures, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 3 , August 2022 , pp. 760 - 774
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chirka, E., The Lindelöf and Fatou theorems in $\mathbb {C}^{n}$, Math. U.S.S.R Sb. 21 (1973), 619–641.Google Scholar
Forstnerič, F., Admissible boundary values of bounded holomorphic functions in wedges, Trans. Amer. Math. Soc. 332 (1992), 583–593.CrossRefGoogle Scholar
Gromov, M., Pseudoholomorphic curves in symplectic manifolds, Invent. Math. 82 (1985), 307–347.CrossRefGoogle Scholar
Khurumov, Y., On the Lindelof theorem in $\mathbb {C}^{n}$, Dokl. Akad Nauk SSSR 273 (1983), 1325–1328.Google Scholar
Nagel, A. and Rudin, W., Local boundary behavior of bounded holomorphic functions, Can. J. Math. 30 (1978), 583–592.CrossRefGoogle Scholar
Newlander, A. and Nirenberg, L., Complex analytic coordinates in almost complex manifolds, Ann. Math. 65 (1957), 391–404.CrossRefGoogle Scholar
Nijenhuis, A. and Woolf, W., Some integration problems in almost – complex and complex manifolds, Ann. Math. 77 (1963), 424–489.CrossRefGoogle Scholar
Nirenberg, L., Webster, S. and Yang, P., Local boundary regularity of holomorphic mappings, Commun. Pure Appl. Math. 33 (1980), 305–338.CrossRefGoogle Scholar
Pinchuk, S. and Khasanov, S., Asymptotically holomorphic functions and their applications, Mat. USSR Sb. 62 (1989), 541–550.CrossRefGoogle Scholar
Rosay, J.-P., A propos des ‘wedges’ et d’ ‘edges’ et de prolongements holomorphes, Trans. Amer. Math. Soc. 297 (1986), 63–72.Google Scholar
Sadullaev, A., A boundary uniqueness theorem in $\mathbb {C}^{n}$, Matem. Sb. 101 (1976), 568–583. doi: 10.1017/S1446788719000119.Google Scholar
Sukhov, A, Pluripolar sets, real submanifolds and pseudoholomorphic discs, J. Australian Math. Soc. 109 (2019), 1–19.Google Scholar
Sukhov, A., The Chirka-Lindelof and Fatou type theorems for $\overline \partial _J$-subsolutions, Revista Math. Iberoamericana 36 (2020), 1469–1487.CrossRefGoogle Scholar
Sukhov, A. and Tumanov, A., Filling hypersurfaces by discs in almost complex manifolds of dimension 2, Indiana Univ. Math. J. 57 (2008), 509–544.CrossRefGoogle Scholar