No CrossRef data available.
Article contents
On the Failure of Heilermann's Theorem
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The theorem of Heilermann can be stated thus:—
If the series
is converted into a continued fraction of the form
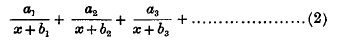
then the elements of the continued fraction are
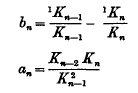
where
and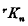 
is obtained from this determinant by deleting the (r + 1)th column and the last row.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1917
References
page 83 note * Journal für Math. 33 (1845), p. 174.Google Scholar
page 87 note * Thus, even if p be ∞, the third relation of (6) will not hold unless A 2 = a 5.
page 89 note * On the Theory of Continued Fractions, Proc. Edin. Math. Soc., 34 Part (2), 1916–1917.Google Scholar
page 90 note * It is also evident from the relation
F(α, β, γ, x) = (1−x)γ−α−βF(γ−α, γ−β, γ, x) due to Euler.
page 94 note * Sur un certain systéme d'équations linéares. Journ. (de Liouville) de Math. (2), iii., p. 46.Google Scholar
page 95 note * See Section (O), “On the Theory of Continued Fractions” (2nd Paper), Proc. Edin. Math. Soc. 35 (Part I.), 1916–1917, p. 48.Google Scholar
page 96 note * This is evidently the case of 
due to Gauss.
page 97 note * Evidently (n−r) in number, for in others all the elements of the first row are zero.
page 98 note * Memoire sur l'élimination. Annales de l'École Norm. Sup. (2) 7 (1878), p. 151.CrossRefGoogle Scholar
page 98 note † The C's with suffixes higher than n are to be replaced by zeros.
page 99 note * If n is odd, m is odd also ; if n is odd and m even, then at least two of the convergents are equal, but they may not be the n th and the m th convergent.
page 100 note * The conditions are sufficient if none of the a's is zero.
page 102 note * K (a 2a 3 …) denotes the continuant 
You have
Access