Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T02:55:19.034Z Has data issue: false hasContentIssue false
  • English
  • Français

On the essential spectrum of Banach-space operators

Published online by Cambridge University Press:  20 January 2009

Jörg Eschmeier
Jörg Eschmeier
Affiliation:
Fachbereich Mathematik, Universität des Saarlandes, D-66123 Saarbrücken, Germany
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T and S be quasisimilar operators on a Banach space X. A well-known result of Herrero shows that each component of the essential spectrum of T meets the essential spectrum of S. Herrero used that, for an n-multicyclic operator, the components of the essential resolvent set with maximal negative index are simply connected. We give new and conceptually simpler proofs for both of Herrero's results based on the observation that on the essential resolvent set of T the section spaces of the sheaves

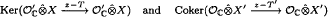
are complete nuclear spaces that are topologically dual to each other. Other concrete applications of this result are given.

Keywords

quasisimilarityessential spectrumcoherent sheavessheaf models
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 43 , Issue 3 , October 2000 , pp. 511 - 528
Copyright
Copyright © Edinburgh Mathematical Society 2000

References

1.Albrecht, E. and Eschmeier, J., Analytic functional models and local spectral theory, Proc. Lond. Math. Soc. 75 (1997), 323–348.CrossRefGoogle Scholar
2.Eschmeier, J., Analytische Dualität und Tensorprodukte in der mehrdimensionalen Spektraltheorie, Schriftenreihe des Math. Inst. der Univ. Münster 42 (1987), 132pp.Google Scholar
3.Eschmeier, J. and Putinar, M., Spectral decompositions and analytic sheaves, London Mathematical Society Monographs, vol. 10 (Clarendon Press, Oxford, 1996).CrossRefGoogle Scholar
4.Finch, J. K., The single-valued extension property on a Banach space, Pacific J. Math. 58 (1975), 61–69.CrossRefGoogle Scholar
5.Grauert, H. and Remmert, R., Theory of Stein spaces (Springer, Berlin, 1979).CrossRefGoogle Scholar
6.Herrero, D., The Fredholm structure of an n-multicyclic operator, Indiana Univ. Math. J. 36 (1987), 549–566.CrossRefGoogle Scholar
7.Herrero, D., On the essential spectra of quasisimilar operators, Can. J. Math. 40 (1988), 1436–1457.CrossRefGoogle Scholar
8.Köthe, G., Topological vector spaces I (Springer, Berlin, 1969).Google Scholar
9.Köthe, G., Topological vector spaces II (Springer, New York, 1979).CrossRefGoogle Scholar
10.Kultze, R., Garbentheorie (Teubner, Stuttgart, 1970).CrossRefGoogle Scholar
11.Miller, T. L. and Miller, V. G., Equality of essential spectra of quasisimilar operators with property (δ), Glasgow Math. J. 38 (1996), 21–28.CrossRefGoogle Scholar
12.Putinar, M., Quasisimilarity of tuples with Bishop's property (β), Integral Eqn. Operator Theory 15 (1992), 1047–1052.CrossRefGoogle Scholar
13.Schaefer, H., Topological vector spaces (Macmillan, New York, 1966).Google Scholar
14.Yang, L., Quasisimilarity of hyponormal and subdecomposable operators, J. Funct. Analysis 112 (1993), 204–217.CrossRefGoogle Scholar