Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:53:27.941Z Has data issue: false hasContentIssue false
  • English
  • Français

On the “elementary” solution of Laplace's Equation

Published online by Cambridge University Press:  20 January 2009

H. S. Ruse
H. S. Ruse
Affiliation:
Edinburgh University.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Hadamard defines the “elementary solution” of the general linear partial differential equation of the second order, namely

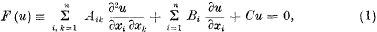
(Aik, BiC being functions of the n variables x1, x2, .., xn, which may be regarded as coordinates in a space of n dimensions), to be one of those solutions which are infinite to as low an order as possible at a given point and on every bicharacteristic through that point.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 2 , Issue 3 , January 1931 , pp. 135 - 139
Copyright
Copyright © Edinburgh Mathematical Society 1931

References

page 135 note 1Lectures on Gauchy's Problem in Linear Partial Differential Equations (Yale, 1923), p. 70, et seq.Google Scholar

page 135 note 2The solutions satisfying this condition differ only in the values of arbitrary constants, the elementary solution being obtained by choosing these according to a certain rule. For the purpose of this paper it suffices to say that the elementary solution is the one which reduces to 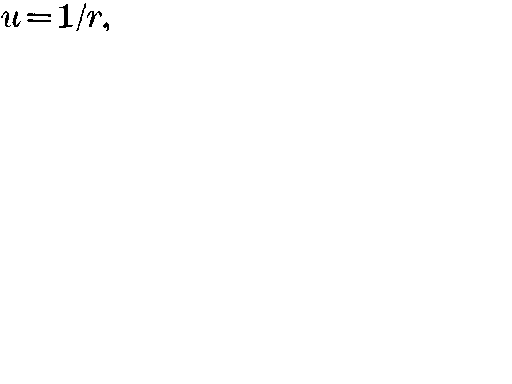, where 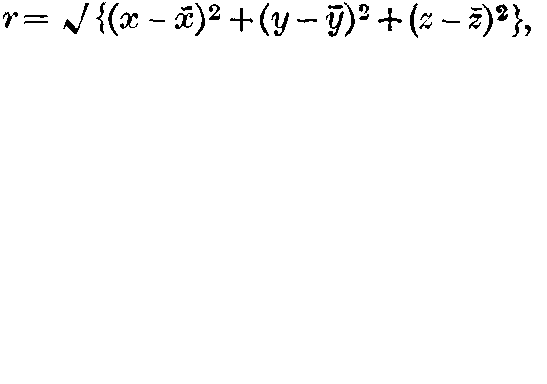, when the differential equation (1) is of the particular form 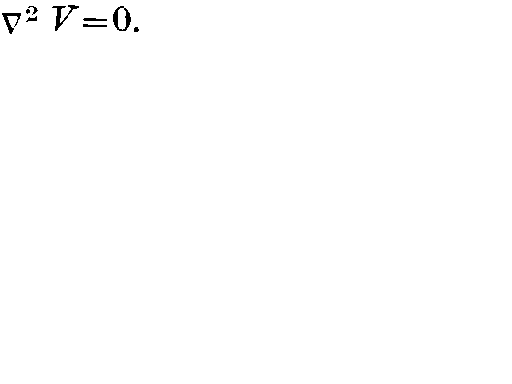.Google Scholar

page 136 note 1The summation convention is adopted throughout. The notation of the succeeding paragraphs will differ to some extent from that of Hadamard, in order that it should be brought into conformity with the notation now usual in the Tensor Calculus.Google Scholar

page 136 note 2 Thus if in § 1 (qi) is taken at 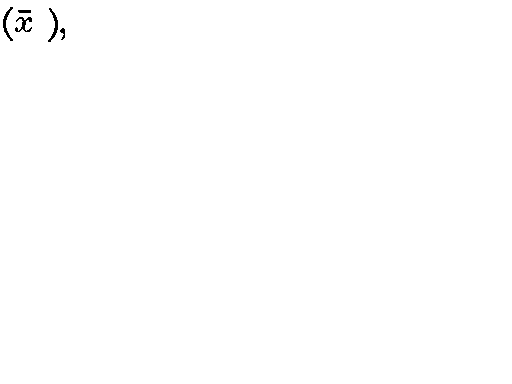, we have .

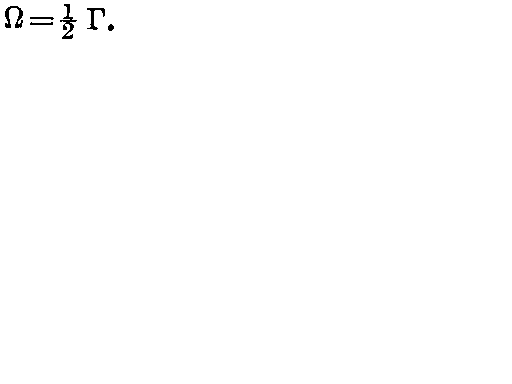page 137 note 1The y i are the normal variables of Lipschitz :Google ScholarHadamard, , loc. cit., p. 87.Google Scholar A full account of them is given by Veblen, , Invariants of Quadratic Differential Forms (Cambridge Tract no. 24, 1927), ch. VI.Google Scholar

page 137 note 2Veblen, , loc. cit., ch. VI (14.8).Google Scholar

page 138 note 1This equation is essentially the same as Hadamard's, loc. cit., p. 91 (37).Google Scholar

page 138 note 2In a paper by the author to appear shortly in Proc. London Math. Soc.Google Scholar