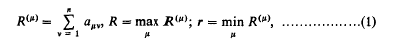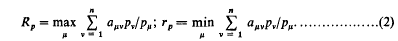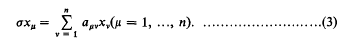Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ostrowski, A. M.
1963.
On positive matrices.
Mathematische Annalen,
Vol. 150,
Issue. 3,
p.
276.
Minc, Henryk
1970.
On the Maximal Eigenvector of a Positive Matrix.
SIAM Journal on Numerical Analysis,
Vol. 7,
Issue. 3,
p.
424.
Brauer, Alfred
and
Gentry, Ivey C.
1976.
Bounds for the greatest characteristic root of an irreducible nonnegative matrix II.
Linear Algebra and its Applications,
Vol. 13,
Issue. 1-2,
p.
109.
1979.
Nonnegative Matrices in the Mathematical Sciences.
p.
298.
Hudson, Richard H.
and
Markham, Thomas L.
1984.
Alfred T. Brauer as a mathematician and teacher.
Linear Algebra and its Applications,
Vol. 59,
Issue. ,
p.
1.
Latham, Geoff A.
and
Anderssen, Robert S.
1994.
Assessing quantification for the EMS algorithm.
Linear Algebra and its Applications,
Vol. 210,
Issue. ,
p.
89.
Latham, Geoff A.
1995.
A Remark on Minc’s Maximal Eigenvector Bound for Positive Matrices.
SIAM Journal on Matrix Analysis and Applications,
Vol. 16,
Issue. 1,
p.
307.
Bapat, R. B.
Olesky, D. D.
and
van den Driessche, P.
1995.
Perron-frobenius theory for a generalized eigenproblem.
Linear and Multilinear Algebra,
Vol. 40,
Issue. 2,
p.
141.
Zhang, Xiao-Dong
and
Luo, Rong
2002.
Upper bound for the non-maximal eigenvalues of irreducible nonnegative matrices.
Czechoslovak Mathematical Journal,
Vol. 52,
Issue. 3,
p.
537.
Zhang, Xiao-Dong
2005.
Eigenvectors and eigenvalues of non-regular graphs.
Linear Algebra and its Applications,
Vol. 409,
Issue. ,
p.
79.
Shi, Lingsheng
2007.
The spectral radii of a graph and its line graph.
Linear Algebra and its Applications,
Vol. 422,
Issue. 1,
p.
58.
Salinelli, Ernesto
and
Sgarra, Carlo
2011.
Some Results on Correlation Matrices for Interest Rates.
Acta Applicandae Mathematicae,
Vol. 115,
Issue. 3,
p.
291.
2015.
Spectral Radius of Graphs.
p.
147.
Wang, Gang
Wang, Yanan
and
Wang, Yiju
2020.
Some Ostrowski-type bound estimations of spectral radius for weakly irreducible nonnegative tensors.
Linear and Multilinear Algebra,
Vol. 68,
Issue. 9,
p.
1817.
Rump, S.M.
2022.
Entrywise lower and upper bounds for the Perron vector.
Linear Algebra and its Applications,
Vol. 653,
Issue. ,
p.
314.
Liao, Ping
2023.
Bounds for the Perron root of positive matrices.
Linear and Multilinear Algebra,
Vol. 71,
Issue. 11,
p.
1849.