Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:33:02.612Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Dvoretzky-Rogers theorem

Published online by Cambridge University Press:  20 January 2009

Fuensanta Andreu
Fuensanta Andreu
Affiliation:
Facultad de Matematicas, Dr. Moliner, 50, Burjasot (Valencia)Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The classical Dvoretzky-Rogers theorem states that if E is a normed space for which l1(E)=l1{E} (or equivalently 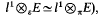, then E is finite dimensional (see [12] p. 67). This property still holds for any lp (l<p<∞) in place of l1 (see [7]p. 104 and [2] Corollary 5.5). Recently it has been shown that this result remains true when one replaces l1 by any non nuclear perfect sequence space having the normal topology (see [14]). In this context, De Grande-De Kimpe [4] gives an extension of the Devoretzky-Rogers theorem for perfect Banach sequence spaces.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 27 , Issue 2 , June 1984 , pp. 105 - 113
Copyright
Copyright © Edinburgh Mathematical Society 1984

References

1.Andreo, F., Espacios escalonados de orden (p,q). (to appear).Google Scholar
2.Apiola, H., Duality between spaces of p-summable sequences, (p,q)-summing operators and characterizations of nuclearity, Math. Ann. 64 (1976), 53–64.Google Scholar
3.De Grande De Kimpe, N., Generalized sequence spaces, Bull. Soc. Math. Belg. 23 (1981), 123–166.Google Scholar
4.De Grande De Kimpe, N., Locally convex spaces for which A(£)=A[JE] and the Dvoretzky-Rogers theorem, Compositio Math. 35 (1977), 139–145.Google Scholar
5.Dubinsky, E., Echelon spaces of order co, Proc. Amer. Math. Soc. 16 (1965), 1178–1183.Google Scholar
6.Dvoretzky, A. and Rogers, C., Absolute and unconditional convergence in normed linear spaces, Proc. Nat. Acad. Sci. U.S.A. 36 (1950), 192-197.Google Scholar
7.Grothendieck, A., Sur certains classes de suites dans les espaces de Banach et le theoreme de Dvoretzky-Rogers, Bol. Soc. Math. Sao Paulo 8 (1956), 81–110.Google Scholar
8.Jarchow, H., Locally Convex Spaces (Stuttgart:B. G. Teubner, 1981).Google Scholar
9.Kothe, G., Topological Vector Spaces I (Berlin-Heidelberg-New York:Springer, 1969).Google Scholar
10.Kothe, G., Topological Vector Spaces II (Berlin-Heidelberg-New York: Springer, 1980).Google Scholar
11.Pietsch, A., Veralgemeinerte volkommene Folgen Räume (Akademie Verlag, 1962).Google Scholar
12.Pietsch, A., Nuclear Locally Convex Spaces (Berlin-Heidelberg-New York:Springer, 1972).Google Scholar
13.Rosier, R. C., Dual spaces of certain vector sequence spaces, Pacific J. Math. 46 (1973), 487–501.Google Scholar
14.Rosier, R. C., Vector sequence spaces and the Dvoretzky-Rogers theorem (to appear).Google Scholar
15.Valdivia, M., Topics in locally convex spaces (Amsterdam-New York-Oxford: Mathematics Studies 67, 1982).Google Scholar