Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:46:40.825Z Has data issue: false hasContentIssue false
  • English
  • Français

On the divisibility of the class number of 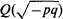by 16

Published online by Cambridge University Press:  20 January 2009

Philip A. Leonard  and
Kenneth S. Williams
Philip A. Leonard
Affiliation:
Department of Mathematics, Arizona State University, Tempe, Arizona 85287, U.S.A.
Kenneth S. Williams
Affiliation:
Department of Mathematics, and Statistics Carleton University, Ottawa, Ontario, Canada K1S 5B6
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let d(<0) denote a squarefree integer. The ideal class group of the imaginary quadratic field has a cyclic 2-Sylow subgroup of order ≦8 in precisely the following cases (see for example [5] and [6]):

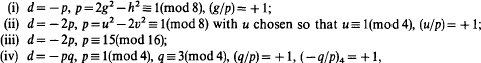
where p and q denote primes and g, h, u and v are positive integers. The class number of is denoted by h(d) and in the above cases h(d) = 0(mod 8). For cases (i), (ii) and (iii) the authors [6] have given necessary and sufficient conditions for h(d) to be divisible by 16. In this paper we do the same for case (iv) extending the results of Brown [4].

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 26 , Issue 2 , June 1983 , pp. 221 - 231
Copyright
Copyright © Edinburgh Mathematical Society 1983

References

REFERENCES

1.Bauer, H., Zur Berechnung der 2-Klassenzahl der quadratische Zahlkörper mit genau zwei verschiedenen Diskriminantenprimteilern, J. Reine Angew. Math. 248 (1971), 42–46.Google Scholar
2.Brown, Ezra, The power of 2 dividing the class-number of a binary quadratic discriminant, J. Number Theory 5 (1973), 413–419.CrossRefGoogle Scholar
3.Brown, Ezra, Class numbers of complex quadratic fields, J. Number Theory 6 (1974), 185–191.CrossRefGoogle Scholar
4.Brown, Ezra, The class-number of for p≡ – q ≡1(mod 4) primes, Houston J. Math. 7 (1981), 497–505.Google Scholar
5.Kaplan, Pierre, Divisibilité par 8 du nombre des classes des corps quadratiques dont le 2-groupe des classes est cyclique, et réciprocité biquadratique, J. Math. Soc. Japan 25 (1973), 596–608.Google Scholar
6.Leonard, Philip A. and Williams, Kenneth S., On the divisibility of theclass numbers of and by 16, Canad. Math. Bull. 25 (1982), 200–206.CrossRefGoogle Scholar
7.Nagell, Trygve, Introduction to Number Theory, (reprinted, Chelsea Publishing Company, New York, 1964).Google Scholar