Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-29T13:05:39.674Z Has data issue: false hasContentIssue false
  • English
  • Français

On the difference of two fourth powers

Part of: Arithmetic problems. Diophantine geometry Curves

Published online by Cambridge University Press:  10 November 2023

Nguyen Xuan Tho Open the ORCID record for Nguyen Xuan Tho [Opens in a new window]
Nguyen Xuan Tho*
Affiliation:
Hanoi University of Science and Technology Hanoi, Vietnam ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the equation 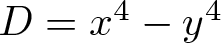$D=x^4-y^4$ in field extensions. As an application, for a prime number p, we find solutions to 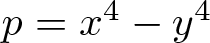$p=x^4-y^4$ if 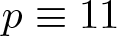$p\equiv 11$ (mod 16) and 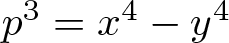$p^3=x^4-y^4$ if 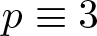$p\equiv 3$ (mod 16) in all cubic extensions of 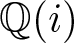$\mathbb{Q}(i)$.

Keywords

Diophantine equationsquartic curvessolutions in field extensions

MSC classification

Primary: 14G25: Global ground fields
Secondary: 14H50: Plane and space curves
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 67 , Issue 1 , February 2024 , pp. 142 - 150
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bajolet, A., Dupuy, B., Luca, F. and Togbe, A., On the Diophantine equation $x^4- q^4=py^r$, Publ. Math. Debrecen 79 (2011), 269–282.CrossRefGoogle Scholar
Bennett, M. A., Integers presented by $x^4-y^4$ revisited, Bull. Aust. Math. Soc. 76 (2007), 133–136.Google Scholar
Bremner, A., Some quartic curves with no points in any cubic field, Proc. Lond. Math. Soc. 52(3): (1986), 193–214.CrossRefGoogle Scholar
Cao, Z., The Diophantine equations $x^4-y^4 = z^p$ and $x^4-1 = dy^q$, C. R. Math. Rep. Acad. Sci. Canada 21 (1999), 23–27.Google Scholar
Cassels, J. W. S., The arithmetic of certain quartic curves, Proc. Roy. Soc. Edinburgh Sect. A 100(3–4) (1985), 201–218.CrossRefGoogle Scholar
Dabrowski, A., On the integers represented by $x^4-y^4$, Bull. Aust. Math. Soc. 76 (2007), 133–136.CrossRefGoogle Scholar
Darmon, H., The equation $x^4-y^4= z^p$, C. R. Math. Rep. Acad. Sci. Canada 15(6) (1993), 286–290.Google Scholar
Faltings, G., Endlichkeitssätze für abelsche Varietä ten über Zahlkörpern, Invent. Math. 73(3) (1983), 349–366.CrossRefGoogle Scholar
Izadi, F., Naghdali, R. F. and Brown, P. G., Some quartic Diophantine equations in Gaussian integers, Bull. Aust. Math. Soc. 92 (2015), 187–194.CrossRefGoogle Scholar
Mondal, P., How many zeroes? Counting Solutions of Systems of Polynomials via Toric Geometry at Infinity. CMS/CAIMS Books in Mathematics, Volume 2 (Switzerland: Springer, 2021).CrossRefGoogle Scholar
Savin, D., On the Diophantine equation $x^4-q^4=py^5$, Ital. J. Pure Appl. Math. 26 (2009), 103–108.Google Scholar
Serre, J. P., Topics in Galois Theory, Research Notes in Mathematics, Book 1, 2nd edition (Natick, MA: A K Peters/CRC Press, 2016).CrossRefGoogle Scholar
Silverman, J. H., Rational points on certain families of curves of genus at least two, Proc. Lond. Math. Soc. 55 (1987), 465–481.CrossRefGoogle Scholar