Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T06:37:12.229Z Has data issue: false hasContentIssue false
  • English
  • Français

On the continued fractions which represent the functions of Hermite and other functions defined by differential equations

Published online by Cambridge University Press:  20 January 2009

E. T. Whittaker
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The functions of Hermite, which are the same as the functions associated with the parabolic cylinder in harmonic analysis, may be defined* by the differential equation which they satisfy, namely,

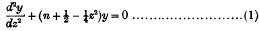
where n denotes any constant.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 32 , February 1913 , pp. 65 - 74
Copyright
Copyright © Edinburgh Mathematical Society 1913

References

* Cf. Hermite, , Comples Sendus 58 (1864), pp. 93, 266.Google Scholar

Whittker, , Proc. Load. Math. Soc. 35 (1903), p. 417.Google Scholar

Myller-Lebedeff, , Math. Ann. 64 (1907), p. 388.CrossRefGoogle Scholar

Watson, , Proc. Land. Math. Soc. (2) 8 (1910), p. 393.CrossRefGoogle Scholar

Curzon, , Proc. Load. Math. Soc. (2) 12 (1912), p. 236.Google Scholar

* Cf. a paper by the present writer in Bull. Amir. Math. Soc. (2) 10 (1903), p. 126.Google Scholar