Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hyslop, J. M.
1939.
Some theorems on absolute Cesàro summability.
Proceedings of the Edinburgh Mathematical Society,
Vol. 6,
Issue. 2,
p.
114.
Hyslop, J. M.
1939.
Some sufficient conditions for the absolute Cesàro summability of series.
Proceedings of the Edinburgh Mathematical Society,
Vol. 6,
Issue. 1,
p.
51.
Hyslop, J. M.
1940.
Note on certain related conditions in the theory of Cesaro summability.
Proceedings of the Edinburgh Mathematical Society,
Vol. 6,
Issue. 3,
p.
165.
Bhatnagar, S. P.
1941.
On the Fourier coefficients of a discontinuous function.
Proceedings of the Edinburgh Mathematical Society,
Vol. 6,
Issue. 4,
p.
231.
Gaier, D.
and
Zeller, K.
1954.
Über deno-umkehrsatz für dasC k-Verfahren.
Rendiconti del Circolo Matematico di Palermo,
Vol. 3,
Issue. 1,
p.
83.



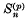 denotes, as usual, the
denotes, as usual, the 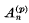 the binomial coefficient
the binomial coefficient 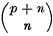 . It is convenient to state here some properties of
. It is convenient to state here some properties of 