Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T16:34:32.445Z Has data issue: false hasContentIssue false
  • English
  • Français

On the algebraicity about the Hodge numbers of the Hilbert schemes of algebraic surfaces

Part of: Discontinuous groups and automorphic forms Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  19 April 2022

Seokho Jin  and
Sihun Jo Open the ORCID record for Sihun Jo [Opens in a new window]
Seokho Jin
Affiliation:
Department of Mathematics, Chung-Ang University, 84 Heukseok-ro, Dongjak-gu, Seoul 06974, Republic of Korea ([email protected])
Sihun Jo
Affiliation:
Department of Mathematics Education, Woosuk University, 443 Samnye-ro, Samnye-eup, Wanju-Gun, Jeollabuk-do 55338, Republic of Korea ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Hilbert schemes are an object arising from geometry and are closely related to physics and modular forms. Recently, there have been investigations from number theorists about the Betti numbers and Hodge numbers of the Hilbert schemes of points of an algebraic surface. In this paper, we prove that Göttsche's generating function of the Hodge numbers of Hilbert schemes of $n$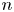 points of an algebraic surface is algebraic at a CM point $\tau$ 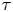and rational numbers $z_1$ 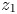and $z_2$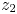. Our result gives a refinement of the algebraicity on Betti numbers.

Keywords

Hodge numberalgebraicityHilbert scheme

MSC classification

Primary: 11R04: Algebraic numbers; rings of algebraic integers
Secondary: 11G16: Elliptic and modular units 11F50: Jacobi forms
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 2 , May 2022 , pp. 392 - 403
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvarez-Gaumé, L., Moore, G. and Vafa, C., Theta functions, modular invariance, and strings, Commun. Math. Phys. 106 (1986), 1–40.CrossRefGoogle Scholar
Beliakova, A., Chen, Q. and Le, T., On the integrality of the Witten-Reshetikhin-Turaev 3-manifold invariants, Quantum Topol. 5 (2014), 99–141.CrossRefGoogle Scholar
Berndt, B. C., Chan, H. H. and Zhang, L. C., Explicit evaluations of the Rogers-Ramanujan continued fraction, J. Reine Angew. Math. 480 (1996), 141–159.Google Scholar
Berndt, B. C., Chan, H. H. and Zhang, L. C., Ramanujan's remarkable product of theta-function, Proc. Edinb. Math. Soc. 40 (1997), 583–612.CrossRefGoogle Scholar
Bonora, L., Bytsenko, A. and Elizalde, E., String partition functions, Hilbert schemes and affine Lie algebra representations on homology groups, J. Phys. A: Math. Theor. 45 (2012), 374002.CrossRefGoogle Scholar
Bringmann, K., Craig, W., Males, J. and Ono, K., Distributions on partitions arising from Hilbert schemes and hook lengths, available at https://arxiv.org/abs/2109.10394.Google Scholar
Bringmann, K. and Manschot, J., Asymptotic formulas for coefficients of inverse theta functions, Commun. Number Theory Phys. 7(3) (2013), 497–513.CrossRefGoogle Scholar
Gillman, N., Gonzalez, X. and Schoenbauer, M., Exact formulas for invariants of Hilbert schemes, Res. Number Theory 4 (2018), 39.CrossRefGoogle Scholar
Gillman, N., Gonzalez, X., Ono, K., Rolen, L. and Schoenbauer, M., From partitions to Hodge numbers of Hilbert schemes of surfaces, Phil. Trans. R, Soc. A 378 (2019), 20180435.CrossRefGoogle ScholarPubMed
Göttsche, L., Hilbert schemes of zero-dimensional subschemes of smooth varieties, Lecture Notes in Mathematics, 1572 (Springer-Verlag, Berlin, 1994).CrossRefGoogle Scholar
Griffin, M. J., Ono, K., Rolen, L. and Tsai, W.-Y., Limiting Betti distributions of Hilbert schemes on $n$ points, available at https://arxiv.org/abs/2112.05279.Google Scholar
Griffin, M. J., Ono, K. and Warnaar, S. O., A framework of Rogers-Ramanujan identities and their arithmetic properties, Duke Math. J. 165(8) (2016), 1475–1527.CrossRefGoogle Scholar
Griffiths, P. and Harris, J., Principles of algebraic geometry, Pure and Applied Mathematics. Wiley-Interscience (John Wiley & Sons, New York, 1978).Google Scholar
Grothendieck, A., Techniques de construction et théorémes d'existence en géométrie algébrique. IV. Les schémas de Hilbert, Séminaire Bourbaki : années 1960/61, exposés 205-222, Séminaire Bourbaki, no. 6 (1961), Exposé no. 221, 28 p.Google Scholar
Gukov, S. and Vafa, C., Rational conformal field theories and complex multiplication, Commun. Math. Phys. 246 (2004), 181–210.CrossRefGoogle Scholar
Jin, S. and Jo, S., The asymptotic formulas for coefficients and algebraicity of Jacobi forms expressed by infinite product, J. Math. Anal. Appl. 471 (2019), 623–646.CrossRefGoogle Scholar
Kanno, K. and Watari, T., Revisiting arithmetic solutions to the $W=0$ condition, Phys. Rev. D 96 (2017), 106001.CrossRefGoogle Scholar
Koo, J. K., Shin, D. H. and Yoon, D. S., Algebraic integers as special values of modular units, Proc. Edinb. Math. Soc. 55 (2012), 167–179.CrossRefGoogle Scholar
Kubert, D. S. and Lang, S., Modular units, Grundlehren Math. Wiss. 244 (Springer, New York, 1981).CrossRefGoogle Scholar
Manschot, J. and Rolon, J. M. Z., The asymptotic profile of $\chi _y$-genera of Hilbert schemes of points on K3 surfaces, Commun. Number Theory Phys. 9(2) (2015), 413–436.CrossRefGoogle Scholar
Nakajima, H., Lectures on Hilbert schemes of points on surfaces, University Lecture Series, Volume 18 (American Mathematical Society, Providence, RI, 1999).CrossRefGoogle Scholar
Ramanujan, S., Notebooks (2 volumes) (Tata Institute of Fundamental Research, Bombay, 1957).Google Scholar
Vafa, C. and Witten, E., A Strong coupling test of S duality, Nucl. Phys. B431 (1994), 3–77.CrossRefGoogle Scholar