Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bosanquet, L. S.
and
Hyslop, J. M.
1937.
On the absolute summability of the Allied series of a fourier series.
Mathematische Zeitschrift,
Vol. 42,
Issue. 1,
p.
489.
Boyd, A. V.
and
Hyslop, J. M.
1952.
A Definition for Strong Rieszian Summability and its Relationship to Strong Cesaro Summability.
Proceedings of the Glasgow Mathematical Association,
Vol. 1,
Issue. 2,
p.
94.
Borwein, D.
1959.
An extension of a theorem on the equivalence between absolute Rieszian and absolute Cesàro summability.
Proceedings of the Glasgow Mathematical Association,
Vol. 4,
Issue. 2,
p.
81.
Bhatt, Shri Nivas
1959.
An aspect of local property of $\vert R,\,{\rm log}\,n,\,1\vert $ summability of Fourier series.
Tohoku Mathematical Journal,
Vol. 11,
Issue. 1,
Srivastava, Pramila
1960.
On the summability of the Dirichlet's product of summable series.
Archiv der Mathematik,
Vol. 11,
Issue. 1,
p.
342.
Srivastava, Pramila
1960.
Tauberian theorems for absolute summability of series and integrals.
Mathematische Zeitschrift,
Vol. 73,
Issue. 5,
p.
460.
Bhatt, Shri Nivas
1962.
An aspect of local property of absolute summability of the derived Fourier series.
Mathematische Zeitschrift,
Vol. 80,
Issue. 1,
p.
384.
Boyer, B. J.
and
Holder, L. I.
1963.
A generalization of absolute Rieszian summability.
Proceedings of the American Mathematical Society,
Vol. 14,
Issue. 3,
p.
459.
Maddox, Ivor J.
1963.
On absolute Riesz summability factors, I.
Tohoku Mathematical Journal,
Vol. 15,
Issue. 2,
Kulsherstha, G. C. N.
1965.
Absolute riesz summability factors of infinite series.
Mathematische Zeitschrift,
Vol. 86,
Issue. 5,
p.
365.
Ratti, J. S.
1966.
On high indices theorems.
Proceedings of the American Mathematical Society,
Vol. 17,
Issue. 5,
p.
1001.
Ratti, J. S.
1967.
Tauberian theorems for absolute summability.
Proceedings of the American Mathematical Society,
Vol. 18,
Issue. 5,
p.
775.
Ratti, J. S.
1969.
On a relation between absolute Abel and absolute Riesz summability..
Proceedings of the American Mathematical Society,
Vol. 21,
Issue. 1,
p.
57.
Nurullah Rasedee, Ahmad Fadly
Ahmedov, Anvarjon
and
Abdul Sathar, Mohammad Hasan
2017.
Asymptotic formula for the Riesz means of the spectral functions of Laplace-Beltrami operator on unit sphere.
Journal of Physics: Conference Series,
Vol. 890,
Issue. ,
p.
012117.


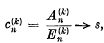
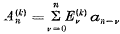
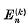 is defined formally by the relation
is defined formally by the relation