Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T06:35:23.000Z Has data issue: false hasContentIssue false
  • English
  • Français

On strong integral summability

Published online by Cambridge University Press:  20 January 2009

E. C. Heagy  and
B. L. R. Shawyer
E. C. Heagy
Affiliation:
Division of Physical Sciences, Scarborough College, University of Toronto, Toronto, Ontario, Canada, M1C 1A4.
B. L. R. Shawyer
Affiliation:
Department of Mathematics, University of Western Ontario, London, Ontario, Canada, N6A 5B9.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Strong summability has been studied by many authors, including Borwein and Cass (1, 2) who have studied sequence-to-sequence transforms. Here we studyintegral transforms; and due to the lack of a limitation theorem for such transforms, some results do not follow directly as in the sequence cases. The strong methods defined here can be applied to construct known and new strong summability methods. We do not give details here, but refer the reader to (3) with the suggestion that the natural scale operator method be used for Q and the named method for P. For example, with the Cesà methods, let P=(C,k,δ) and Q=(C,δ) to obtain .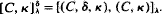

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 21 , Issue 1 , March 1978 , pp. 73 - 78
Copyright
Copyright © Edinburgh Mathematical Society 1978

References

REFERENCES

(1) Borwein, D., On strong and absolute summability, Proc. Glasgow Math. Assoc. 4 (1960), 122–139.CrossRefGoogle Scholar
(2) Borwein, D. and Cass, F. P., Strict inclusion between strong and ordinary methods of summability, J. Reine Angew. Math., 267 (1974), 166–174.Google Scholar
(3) Shawyer, B. L. R., Iteration products of methods of summability and natural scales, Manuscripta Math. 13 (1974), 355–364.CrossRefGoogle Scholar