Ellipsoidal harmonics are defined to be those solutions of Laplace's equation

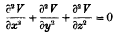
(where x, y, z are rectangular coordinates) which are useful in problems relating to ellipsoids. If the equation

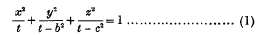
represents a family of confocal quadrics, it is known that the ellipsoidal harmonics belonging to the family are products of the form

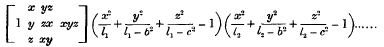
where l1, l2… are constants: one term is to be picked out of the square brackets as a multiplier of the other factors. Now if we consider the case in which two of the principal axes of the ellipsoids are equal, the latter become spheroids. If then we put b = 0 in (1) the family of confocal spheroids has the equation

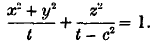
and belonging to this family there will be spheroidal harmonics of the form given by (2) with b zero.