No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
The number of groups of n which may be selected from 2n is 2n(2n − l)…(n + l)/n! But make the 2n into two groups of n, and select r out of the first and n − r out of the second. This gives [n(n−l)…(n−r+l)/r!] + [n(n−l)…(r + l)/(n−r)!] ways of thus making a group of n. Hence
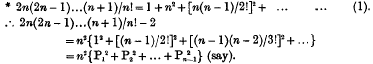
* The use of this identity was suggested to me by Professor Tait.
* Compare a paper by MrLeudesdorf, , in the Proceedings of the Lond. Math. Soc. for 1889, p. 199–a paper which I did not see till after the above was written.Google Scholar
You have
Access