No CrossRef data available.
Article contents
On some results concerning integral equations
Published online by Cambridge University Press: 20 January 2009
Extract
It is proposed in this paper to show now the well-known Laplace's transformation,
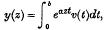
which is of great help in finding the solution of linear differential equations, gives also interesting results concerning the theory of integral equations. In §2 we shall study its application to certain differential equations, and find a large class of equations which remain unchanged by this transformation. Then, (§3), taking instead of eazt, a more general function of the product zt, we shall find a solution for some homogeneous integral equations ; in § 4 we shall describe a method of solving a very general type of integral equation of the first kind, namely,
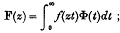
a further extension to integral equations with the kernel ef(z)f(t) the object of §5. Then, studying an extension of Euler's transformation, we shall (§ 6) consider equations such as
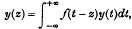
which will prove to be singular; and finally, in §7, we shall give other examples of singular integral equations.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1913


