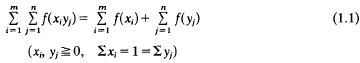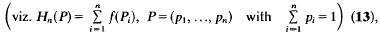Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kannappan, Pl.
1985.
On a generalization of sum form functional equation—V.
Aequationes Mathematicae,
Vol. 28,
Issue. 1,
p.
255.
Sander, Wolfgang
1986.
Weighted-additive deviations with the sum property.
Manuscripta Mathematica,
Vol. 55,
Issue. 3-4,
p.
373.
Sander, Wolfgang
1986.
On a functional equation arising in information theory.
Manuscripta Mathematica,
Vol. 54,
Issue. 4,
p.
439.
Aczél, J.
1987.
Uncertainty in Knowledge-Based Systems.
Vol. 286,
Issue. ,
p.
357.
Kannappan, Pl.
1987.
Uncertainty in Knowledge-Based Systems.
Vol. 286,
Issue. ,
p.
385.
Losonczi, L.
1993.
Measurable solutions of functional equations of sum form.
Acta Mathematica Hungarica,
Vol. 61,
Issue. 1-2,
p.
165.
Ebanks, Bruce R.
Kannappan, Palaniappan
Sahoo, Prasanna K.
and
Sander, Wolfgang
1997.
Characterizations of sum form information measures on open domains.
Aequationes Mathematicae,
Vol. 54,
Issue. 1-2,
p.
1.
Losonczi, László
1997.
A structure theorem for sum form functional equations.
Aequationes Mathematicae,
Vol. 53,
Issue. 1-2,
p.
141.
Kannappan, PL.
and
Sahoo, P. K.
2003.
Entropy Measures, Maximum Entropy Principle and Emerging Applications.
Vol. 119,
Issue. ,
p.
253.
Nath, Prem
2004.
On the measurable solutions of a functional equation related to some measures of entropy in information theory.
Journal of Interdisciplinary Mathematics,
Vol. 7,
Issue. 2,
p.
205.
Nath, Prem
2005.
On the measurable solutions of some functional equations useful in information theory.
Journal of Discrete Mathematical Sciences and Cryptography,
Vol. 8,
Issue. 1,
p.
99.
Nath, Prem
and
Kumar Singh, Dhiraj
2006.
On a multiplicative type sum form functional equation and its role in information theory.
Applications of Mathematics,
Vol. 51,
Issue. 5,
p.
495.
Nath, Prem
2006.
On some sum form functional equations related to information theory.
Journal of Interdisciplinary Mathematics,
Vol. 9,
Issue. 1,
p.
1.