Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:43:09.602Z Has data issue: false hasContentIssue false
  • English
  • Français

On radial variation of holomorphic functions with lp Taylor coefficients

Published online by Cambridge University Press:  20 January 2009

D. J. Hallenbeck  and
K. Samotij
D. J. Hallenbeck
Affiliation:
Department of Mathematical SciencesUniversity of DelawareNewark, Delaware 19716
K. Samotij
Affiliation:
Instytut MatematykiPolitechniki WroclawskiejWybrzeŻc St. Wyspiańskiego 27Wroclaw, Poland
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose 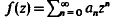is holomorphic in Δ = {z:|z|<l} and (an)∈lp where 1≦p≦2. We prove that 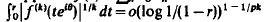for k=1,2,…, and almost every θ. This result is sharp in the following sense: Let p∈[1,2] and ε(r) be a positive function defined on [0,1] such that limr→1-ε(r)=0. Then there exists a function 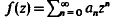holomorphic in Δ with (an)∈lp such that

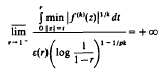
for each k>1/p.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 33 , Issue 3 , October 1990 , pp. 475 - 481
Copyright
Copyright © Edinburgh Mathematical Society 1990

References

REFERENCES

1.Duren, P. L., Theory of Hp Spaces (Academic Press, 1970).Google Scholar
2.Zygmund, A., On certain integrals, Trans. Amer. Math. Soc. 55 (1944), 170–204.CrossRefGoogle Scholar
3.Zygmund, A., Trigonometric Series, Vol 2, 2nd Ed. (Cambridge University Press, London and New York, 1968).Google Scholar