Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T00:38:26.228Z Has data issue: false hasContentIssue false
  • English
  • Français

On Professor Whittaker's solution of differential equations by definite integrals: Part II

Applications of the methods of non-commutative Algebra

Published online by Cambridge University Press:  20 January 2009

W. O. Kermack  and
W. H. McCrea
W. O. Kermack
Affiliation:
(Royal College of Physicians, Edinburgh)
W. H. McCrea
Affiliation:
(Edinburgh University)
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In Part I it has been shown that, given a contact transformation, two equations

can be derived which lead to the compatible differential equations

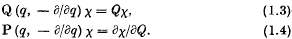
It will be shown in the present communication that the necessary and sufficient condition that (1.3), (1.4) should be compatible is that

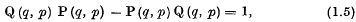
regarded as an equation in the non-commutative variables q, p which themselves satisfy the condition

We shall call functions satisfying this condition conjugate functions. From this point of view the method employed by Professor Whittaker in his original paper, involving the use of a contact transformation,, was really a particular method of generating conjugate functions. This powerful method may be supplemented and extended by the other methods developed in the following pages.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 2 , Issue 4 , June 1931 , pp. 220 - 239
Copyright
Copyright © Edinburgh Mathematical Society 1931

References

page 222 note 1 Dirac, , Principles of Quantum Mechanics (1930), 34. The present algebra differs from Dirac's only in taking qp–pq = 1 instead of qp–pq = i. In some previous work Dirac used the first relation,Google Scholarcf. Proc. Camb. Phil. Soc., 23 (1936), 412.Google Scholar

page 222 note 2 Dirac, , Op. cit., 41.Google Scholar

page 233 note 1 A particular example of this is k = q, h = p, which gives the type of transformation used by Professor Whittaker in § 7 of his paper.

page 236 note 1 Dirac, , op. cit., 63.Google Scholar

page 236 note 2 Recalling the remarks in § 2 on the type of function used.

page 239 note 1 H. W., Turnbull, Proc. Edin. Math. Soc. (2) 2 (1930), 33.Google Scholar