Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-27T13:31:11.205Z Has data issue: false hasContentIssue false
  • English
  • Français

On Liouville theorems of a Hartree–Poisson system

Part of: Singular integral equations Elliptic equations and systems Nonlinear integral equations Partial differential equations

Published online by Cambridge University Press:  26 October 2023

Ling Li  and
Yutian Lei Open the ORCID record for Yutian Lei [Opens in a new window]
Ling Li
Affiliation:
Institute of Mathematics, School of Mathematical Sciences, Nanjing Normal University, Nanjing, China ([email protected]; [email protected])
Yutian Lei
Affiliation:
Institute of Mathematics, School of Mathematical Sciences, Nanjing Normal University, Nanjing, China ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we are concerned with the non-existence of positive solutions of a Hartree–Poisson system: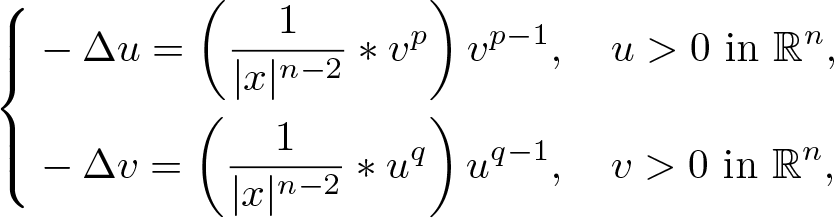

\begin{equation*}\left\{\begin{aligned}&-\Delta u=\left(\frac{1}{|x|^{n-2}}\ast v^p\right)v^{p-1},\quad u \gt 0\ \text{in} \ \mathbb{R}^{n},\\&-\Delta v=\left(\frac{1}{|x|^{n-2}}\ast u^q\right)u^{q-1},\quad v \gt 0\ \text{in} \ \mathbb{R}^{n},\end{aligned}\right.\end{equation*}
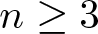where $n \geq3$ and 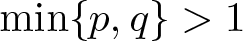$\min\{p,q\} \gt 1$. We prove that the system has no positive solution under a Serrin-type condition. In addition, the system has no positive radial classical solution in a Sobolev-type subcritical case. In addition, the system has no positive solution with some integrability in this Sobolev-type subcritical case. Finally, the relation between a Liouville theorem and the estimate of boundary blowing-up rates is given.

Keywords

Hartree–Poisson systemLiouville theoremradial solutionsmethod of moving planes

MSC classification

Primary: 35J60: Nonlinear elliptic equations 35B33: Critical exponents 45E10: Integral equations of the convolution type (Abel, Picard, Toeplitz and Wiener-Hopf type) 45G15: Systems of nonlinear integral equations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 4 , November 2023 , pp. 1154 - 1178
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Caffarelli, L. A., Gidas, B. and Spruck, J., Asymptotic symmetry and local behavior of semilinear elliptic equations with critical Sobolev growth, Comm. Pure Appl. Math. 42 (3) (1989), 271–297.CrossRefGoogle Scholar
Caristi, G., D’Ambrosio, L. and Mitidieri, E., Representation formulae for solutions to some classes of higher order systems and related Liouville theorems, Milan J. Math. 76 (2008), 27–67.CrossRefGoogle Scholar
Chen, W. and Li, C., Classification of solutions of some nonlinear elliptic equations, Duke Math. J. 63 (3) (1991), 615–622.CrossRefGoogle Scholar
Chen, W. and Li, C., An integral system and the Lane–Emden conjecture, Discrete Contin. Dyn. Syst. 24 (4) (2009), 1167–1184.CrossRefGoogle Scholar
Chen, W., Li, C. and Ou, B., Classification of solutions for an integral equation, Comm. Pure Appl. Math. 59 (3) (2006), 330–343.CrossRefGoogle Scholar
Clément, P., Manasevich, R. and Mitidieri, E., Positive solution for a quasilinear system via blow-up, Comm. Partial Differential Equations 18 (12) (1993), 2071–2106.CrossRefGoogle Scholar
D’ambrosio, L. and Ghergu, M., Representation formulae for nonhomogeneous differential operators and applications to PDEs, J. Differential Equations 317 (2022), 706–753.CrossRefGoogle Scholar
Dai, W., Fang, Y. and Qin, G., Classification of positive solutions to fractional order Hartree equations via a direct method of moving planes, J. Differential Equations 265 (2018), 2044–2063.CrossRefGoogle Scholar
Dai, W., Huang, J., Qin, Y., Wang, B. and Fang, Y., Regularity and classification of solutions to static Hartree equations involving fractional Laplacians, Discrete Contin. Dyn. Syst. 39 (3) (2019), 1389–1403.CrossRefGoogle Scholar
Du, L. and Yang, M., Uniqueness and nondegeneracy of solutions for a critical nonlocal equation, Discrete Contin. Dyn. Syst. 39 (10) (2019), 5847–5866.CrossRefGoogle Scholar
Fröhlich, J. and Lenzmann, E., Mean-field limit of quantum Bose gases and nonlinear Hartree equation, Séminaire: ÉQuations aux Dérivées Partielles. 2003–2004(No.18) (2004), .Google Scholar
Ghergu, M., Liu, Z., Miyamoto, Y. and Moroz, V., Nonlinear inequalities with double Riesz potentials, Potential Anal. 59 (1) (2023), 97–112.CrossRefGoogle Scholar
Ghergu, M. and Taliaferro, S. D., Asymptotic behavior at isolated singularities for solutions of nonlocal semilinear elliptic systems of inequalities, Calc. Var. Partial Differential Equations 54 (2) (2015), 1243–1273.CrossRefGoogle Scholar
Gidas, B., Ni, W. and Nirenberg, L., Symmetry and related properties via the maximum principle, Comm. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
Gidas, B. and Spruck, J., Global and local behavior of positive solutions of nonlinear elliptic equations, Comm. Pure Appl. Math. 34 (4) (1981), 525–598.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order (Springer-Verlag, New York, 1977).CrossRefGoogle Scholar
Guo, L., Hu, T., Peng, S. and Shuai, W., Existence and uniqueness of solutions for Choquard equation involving Hardy–Littlewood–Sobolev critical exponent, Calc. Var. Partial Differential Equations 58 (4) (2019), .CrossRefGoogle Scholar
Hayman, W. K. and Kennedy, P. B., Subharmonic Functions, Volume I (Academic Press, London, New York, San Francisco, 1976).Google Scholar
Hu, B., Remarks on the blowup estimate for solutions of the heat equation with a nonlinear boundary condition, Differential Integral Equations 9 (5) (1996), 891–901.CrossRefGoogle Scholar
Le, P., Symmetry and classification of solutions to an integral equation of the Choquard type, C. R. Math. Acad. Sci. Paris 357 (11-12) (2019), 878–888.CrossRefGoogle Scholar
Le, P., Liouville theorem and classification of positive solutions for a fractional Choquard type equation, Nonlinear Anal. 185 (2019), 123–141.CrossRefGoogle Scholar
Le, P., Liouville theorems for an integral equation of Choquard type, Commun. Pure Appl. Anal. 19 (2) (2020), 771–783.CrossRefGoogle Scholar
Le, P., On classical solutions to the Hartree equation, J. Math. Anal. Appl. 485 (2) (2020), .CrossRefGoogle Scholar
Le, P., Classical solutions to a Hartree type system, Math. Nachr. 294 (12) (2021), 2355–2366.CrossRefGoogle Scholar
Le, P., Uniqueness of non-negative solutions to an integral equation of the Choquard type, Appl. Anal. 102 (14) (2023), 3861–3873.CrossRefGoogle Scholar
Lei, Y., Qualitative analysis for the static Hartree-type equations, SIAM J. Math. Anal. 45 (1) (2013), 388–406.CrossRefGoogle Scholar
Lei, Y., Liouville theorems and classification results for a nonlocal Schrödinger equation, Discrete Contin. Dyn. Syst. 38 (11) (2018), 5351–5377.CrossRefGoogle Scholar
Li, D., Miao, C. and Zhang, X., The focusing energy-critical Hartree equation, J. Differential Equation 246 (3) (2009), 1139–1163.CrossRefGoogle Scholar
Li, Y. and Zhu, M., Uniqueness theorems through the method of moving spheres, Duke Math. J. 80 (2) (1995), 383–417.CrossRefGoogle Scholar
Lieb, E. and Simon, B., The Hartree–Fock theory for Coulomb systems, Comm. Math. Phys. 53 (3) (1977), 185–194.CrossRefGoogle Scholar
Liu, S., Regularity, symmetry, and uniqueness of some integral type quasilinear equations, Nonlinear Anal. 71 (5-6) (2009), 1796–1806.CrossRefGoogle Scholar
Ma, P., Shang, X. and Zhang, J., Symmetry and nonexistence of positive solutions for fractional Choquard equations, Pacific J. Math. 304 (1) (2020), 143–167.CrossRefGoogle Scholar
Mercuri, C., Moroz, V. and Van Schaftingen, J., Groundstates and radial solutions to nonlinear Schrödinger–Poisson–Slater equations at the critical frequency, Calc. Var. Partial Differential Equations 55 (6) (2016), .CrossRefGoogle Scholar
Mitidieri, E., A rellich type identity and applications, Comm. Partial Differential Equations 18 (1-2) (1993), 125–151.CrossRefGoogle Scholar
Mitidieri, E., Nonexistence of positive solutions of semilinear elliptic systems in ${R^{n}}$, Differential Integral Equations 9 (3) (1996), 465–479.CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J., Nonexistence and optimal decay of supersolutions to Choquard equations in exterior domains, J. Differential Equations 254 (8) (2013), 3089–3145.CrossRefGoogle Scholar
Polacik, P., Quittner, P. and Souplet, P., Singularity and decay estimates in superlinear problems via Liouville-type theorems. I. Elliptic Equations and Systems, Duke Math. J. 139 (3) (2007), 555–579.CrossRefGoogle Scholar
Serrin, J., A symmetry problem in potential theory, Arch. Ration. Mech. Anal. 43 (1971), 304–318.CrossRefGoogle Scholar
Serrin, J. and Zou, H., Non-existence of positive solutions of Lane–Emden systems, Differential Integral Equations 9 (4) (1996), 635–653.CrossRefGoogle Scholar
Souplet, P., The proof of the Lane–Emden conjecture in four space dimensions, Adv. Math. 221 (5) (2009), 1409–1427.CrossRefGoogle Scholar
Stein, E. M., Singular Integrals and Differentiability Properties of Functions (Princeton University Press, 1971).CrossRefGoogle Scholar
Wang, K. and Yang, M., Symmetry of positive solutions for Hartree type nonlocal Lane–Emden system, Appl. Math. Lett. 105 (2020), .CrossRefGoogle Scholar
Yang, J. and Yu, X., Liouville type theorems for Hartree and Hartree–Fock equations, Nonlinear Anal. 183 (2019), 191–213.CrossRefGoogle Scholar