Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T14:47:13.094Z Has data issue: false hasContentIssue false
  • English
  • Français

On inverse categories and transfer in cohomology

Part of: Homological methods Homological algebra Special categories

Published online by Cambridge University Press:  05 December 2012

Markus Linckelmann
Markus Linckelmann*
Affiliation:
Department of Mathematical Sciences, Institute of Mathematics, University of Aberdeen, King's College, Fraser Noble Building, Aberdeen AB24 3UE, UK
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It follows from methods of B. Steinberg, extended to inverse categories, that finite inverse category algebras are isomorphic to their associated groupoid algebras; in particular, they are symmetric algebras with canonical symmetrizing forms.We deduce the existence of transfer maps in cohomology and Hochschild cohomology from certain inverse subcategories. This is in part motivated by the observation that, for certain categories 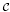, being a Mackey functor on 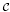is equivalent to being extendible to a suitable inverse category containing 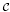. We further show that extensions of inverse categories by abelian groups are again inverse categories.

Keywords

Inverse categorytransfercohomology

MSC classification

Secondary: 18G15: Ext and Tor, generalizations, Künneth formula 18B40: Groupoids, semigroupoids, semigroups, groups (viewed as categories) 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.)
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 1 , February 2013 , pp. 187 - 210
Copyright
Copyright © Edinburgh Mathematical Society 2012

References

1.Baues, H.-J. and Wirsching, G., Cohomology of small categories, J. Pure Appl. Alg. 38 (1985), 187–211.CrossRefGoogle Scholar
2.Broto, C., Levi, R. and Oliver, B., Homotopy equivalences of p-completed classifying spaces of finite groups, Invent. Math. 151 (2003), 611–664.CrossRefGoogle Scholar
3.Broué, M., Higman's criterion revisited, Michigan Math. J. 58 (2009), 125–179.CrossRefGoogle Scholar
4.Dress, A., Contributions to the theory of induced representations, Lecture Notes in Mathematics, Volume 342, pp. 183–240 (Springer, 1973).Google Scholar
5.Gabriel, P. and Zisman, M., Calculus of fractions and homotopy theory, Ergebnisse der Mathematik und Ihrer Grenzgebiete, Volume 35 (Springer, 1967).CrossRefGoogle Scholar
6.Gerstenhaber, M., The cohomology structure of an associative ring, Annals Math. 78 (1963), 267–288.CrossRefGoogle Scholar
7.Grandis, M., Concrete representations for inverse and distributive exact categories, Rend. Accad. Naz. Sci. XL Mem. Mat. 8 (1984), 99–120.Google Scholar
8.Grandis, M., Cohesive categories and manifolds, Annali Mat. Pura Appl. 157 (1990), 199–244.CrossRefGoogle Scholar
9.Isaacs, I. M., Character theory of finite groups (Dover, New York, 1994).Google Scholar
10.Jackowski, S. and McClure, J., Homotopy decomposition of classifying spaces via elementary abelian subgroups, Topology 31 (1992), 113–132.CrossRefGoogle Scholar
11.Jackowski, S. and Słomińska, J., G-functors, G-posets and homotopy decompositions of G-spaces, Fund. Math. 169 (2001), 249–287.CrossRefGoogle Scholar
12.Jackowski, S., McClure, J. and Oliver, B., Homotopy classifications of self-maps of BG via G-actions, II, Annals Math. 135 (1992), 227–270.CrossRefGoogle Scholar
13.Kastl, J., Inverse categories, in Algebraische Modelle, Kategorien und Gruppoide (ed. Hoehnke, H.-J.), pp. 51–60 (Akademie, Berlin, 1979).Google Scholar
14.Lawson, M. V., Inverse semigroups (World Scientific, Singapore, 1998).CrossRefGoogle Scholar
15.Linckelmann, M., Transfer in Hochschild cohomology of blocks of finite groups, Alg. Representat. Theory 2 (1999), 107–135.CrossRefGoogle Scholar
16.Linckelmann, M., Varieties in block theory, J. Alg. 215 (1999), 460–480.CrossRefGoogle Scholar
17.Linckelmann, M., On graded centres and block cohomology, Proc. Edinb. Math. Soc. 52 (2009), 489–514.CrossRefGoogle Scholar
18.Munn, W. D., Matrix representations of semi-groups, Proc. Camb. Phil. Soc. 53 (1957), 5–12.CrossRefGoogle Scholar
19.Ponizovskii, I. S., On matrix representations of associative systems, Mat. Sb. 38 (1956), 241–260.Google Scholar
20.Robinson, E. and Rosolini, G., Categories of partial maps, Inform. Comput. 79 (1988), 95–130.CrossRefGoogle Scholar
21.Steinberg, B., Möbius functions and semigroup representation theory, II, Character formulas and multiplicities, Adv. Math. 217 (2008), 1521–1557.CrossRefGoogle Scholar
22.Webb, P. J., An introduction to the representations and cohomology of categories, in Group representation theory (ed. Geck, M., Testerman, D. and Thévenaz, J.), pp. 149–173 (EPFL Press, Lausanne, 2007).Google Scholar
23.Xu, F., Hochschild and ordinary cohomology rings of small categories, Adv. Math. 219 (2008), 1872–1893.CrossRefGoogle Scholar