Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:46:41.600Z Has data issue: false hasContentIssue false
  • English
  • Français

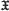On groups which are residually -commutative

Published online by Cambridge University Press:  20 January 2009

David G. Arrell
David G. Arrell
Affiliation:
Leeds Polytechnic, Calverley Street, Leeds LS1 3HE
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study a property which we call residual 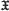-commutativity. This idea was kindled by a paper of Ayoub (1) and one of Stanley (6). Durbin has defined a similar property in (2) which has also been studied by Slotterbeck in (4). Durbin's property implies residual 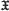-commutativity but we have not been able to decide if they are equivalent. However, we have shown that they coincide in certain circumstances. The notation, unless otherwise stated, is that of Robinson (3).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 20 , Issue 1 , March 1976 , pp. 7 - 13
Copyright
Copyright © Edinburgh Mathematical Society 1976

References

REFERENCES

(1) Ayoub, C., On properties possessed by solvable and nilpotent groups, J. Australian Math. Soc. 9 (1969), 218–227.CrossRefGoogle Scholar
(2) Durbin, J. R., On normal factor coverings of groups, J. Algebra 12 (1969), 191–194.CrossRefGoogle Scholar
(3) Robinson, D. J. S., Finiteness conditions for generalized soluble groups, parts 1 and 2 (Springer-Verlag, Berlin-Heidelberg-New York, 1972).CrossRefGoogle Scholar
(4) Slotterbeck, O. A., Finite factor coverings of groups, J. Algebra 17 (1971), 67–73.CrossRefGoogle Scholar
(5) Stanley, T. E., Generalizations of the classes of nilpotent and hypercentral groups, Math. Z. 118 (1970), 180–190.CrossRefGoogle Scholar
(6) Stanley, T. E., Residual centrality in groups. Math. Z. 126 (1972), 1–5.CrossRefGoogle Scholar