It is well known that the polynomial in x,

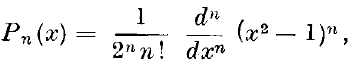
has the following properties:—

(A) it is the coefficient of tn in the expansion of (1–2xt+t2)–½;

(B) it satisfies the three-term recurrence relation

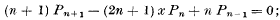
(C) it is the solution of the second order differential equation

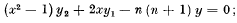
(D) the sequence Pn(x) is orthogonal for the interval (— 1, 1),

i.e. when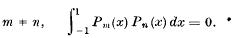

Several other familiar polynomials, e.g., those of Laguerre Hermite, Tschebyscheff, have properties similar to some or all of the above. The aim of the present paper is to examine whether, given a sequence of functions (polynomials or not) which has one of these properties, the others follow from it : in other words we propose to examine the inter-relation of the four properties. Actually we relate each property to the generating function.