Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1980.
Group Representations.
Vol. 180,
Issue. ,
p.
849.
van der Waall, Robert W.
1988.
On the determination of the ramification index in Clifford's theorem.
Proceedings of the Edinburgh Mathematical Society,
Vol. 31,
Issue. 3,
p.
469.
1989.
Clifford Theory for Group Representations.
Vol. 156,
Issue. ,
p.
343.
Loukaki, Maria
2003.
Hyperbolic modules and cyclic subgroups.
Journal of Algebra,
Vol. 266,
Issue. 1,
p.
34.
Jin, Ping
and
Fan, Yun
2015.
Metabolic modules of finite group algebras over finite fields of characteristic two.
Advances in Mathematics,
Vol. 282,
Issue. ,
p.
265.


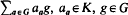 . The action of on α = ∑
. The action of on α = ∑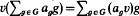 If
If 