Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T06:47:18.186Z Has data issue: false hasContentIssue false
  • English
  • Français

On an Integral due to Ramanujan, and some ideas suggested by it

Published online by Cambridge University Press:  20 January 2009

T. M. MacRobert
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By applying Fourier's Integral Theorem to a well-known formula, due to Cauchy, expressed in the form

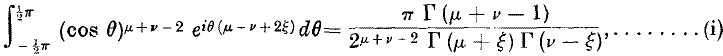
where R (μ + v) > 1, Ramanujan has shown that

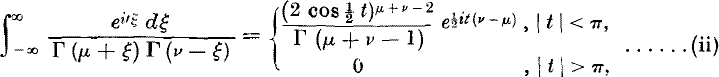
where t is any real number.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 2 , Issue 1 , January 1930 , pp. 26 - 32
Copyright
Copyright © Edinburgh Mathematical Society 1930

References

page 26 note 1 Quart. Journ. of Maths., 48 (1920), 294–310.Google Scholar

page 27 note 1 Whittaker, and Watson, , Modern Analysis, 2nd Ed., p. 309.Google Scholar

page 27 note 2 Proc. Lond. Math. Soc., Ser. 2, 26 (1925), 76.Google Scholar

page 28 note 1 This is a special case of an integral due to Gegenbauer. For references, see Watson, , Bessel Functions, p. 50.Google Scholar

page 29 note 1 Math. Ann., 16 (1880), 39.Google Scholar

page 30 note 1 Gray, , Mathews, , AND MacRobert, , Bessel Functions, p, 66 (11)Google Scholar