I propose to prove the following theorem.

With n > 2, the (n + 2) equations derived from the matrix

where

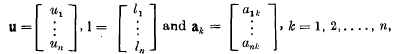
by equating to zero all (n + 1)-rowed determinants from the matrix ‖Δ‖ are equivalent to only two, one of which is linear in li (i = 1, 2, …, n) and the other is homogeneous and quadratic in a certain n – 1 of li (i = 1, 2, …, n); the elements of the matrix are real; 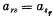(r, s = 1, 2, …, n) and d is arbitrary.