Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T07:18:53.637Z Has data issue: false hasContentIssue false
  • English
  • Français

On a problem of Barnes and Duncan

Published online by Cambridge University Press:  20 January 2009

R. G. McLean
R. G. McLean
Affiliation:
Department of MathematicsThe City UniversityNorthampton Square London EC1V 0HBUnited Kingdom
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the free monoid on a non-empty set P, and let R be the quotient monoid determined by the relations:

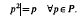
Let R have its natural involution * in which each element of P is Hermitian. We show that the Banach *-algebra ℓ1(R) has a separating family of finite dimensional *-representations and consequently is *-semisimple. This generalizes a result of B. A. Barnes and J. Duncan (J. Funct. Anal.18 (1975), 96–113.) dealing with the case where P has two elements.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 34 , Issue 2 , June 1991 , pp. 321 - 323
Copyright
Copyright © Edinburgh Mathematical Society 1991

References

REFERENCES

1.Bami, M. Lashkarizadeh, Representations of foundation semigroups and their algebras, Canad. J. Math. 37 (1985), 29–47.CrossRefGoogle Scholar
2.Barnes, B. A. and Duncan, J., The Banach algebra l1(S), J. Fund. Anal. 18 (1975), 96–113.CrossRefGoogle Scholar
3.Mclean, R. G. and Kummer, H., Representations of the Banach algebra ll(S), Semigroup forum 37 (1988), 119–122.CrossRefGoogle Scholar