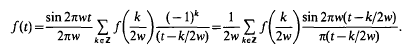Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:26:06.440Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Whittaker's cardinal series in harmonic analysis

Published online by Cambridge University Press:  20 January 2009

M. M. Dodson ,
A. M. Silva  and
V. Soucek
V. Soucek
Affiliation:
Mathematics Department, University of York, Heslington, York Y01 5DD, England Departmento de Fisica, Universitad Nacional de la Plata, Calle 115 y 49—CC No 67, 1900 la Plata, Argentina Katedra Matematicke Analyzy, Charles University, Sokolovska 83, 18600 Praha 8, Czechoslovakia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The sampling theorem, often referred to as the Shannon or Whittaker-Kotel'nikov- Shannon sampling theorem, is of considerable importance in many fields, including communication engineering, electronics, control theory and data processing, and has appeared frequently in various forms in engineering literature (a comprehensive account of its numerous extensions and applications is given in [3]). The result states that a band-limited signal, i.e. a real function f of the form

where w>0, is under reasonable conditions on the even function F, determined by its values on the sampling set (l/2w)ℤ and can be reconstructed from the samples f(k/2w), k∈ℤ, by the series

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 29 , Issue 3 , October 1986 , pp. 349 - 357
Copyright
Copyright © Edinburgh Mathematical Society 1986

References

REFERENCES

1.Dodson, M. M. and Silva, A. M., Fourier analysis and the sampling theorem, Proc. Rov. Irish Acad. 85A (1985), 81–108.Google Scholar
2.Higgins, J. R., Five short stories about the cardinal series, Bull. Amer. Math. Soc. 12 (1985), 45–89.CrossRefGoogle Scholar
3.Jerri, A. J., The Shannon sampling theorem—its various extensions and applications: a tutorial review, Proc. IEEE 65 (1977), 1565–1596.CrossRefGoogle Scholar
4.Kluvanek, I., Sampling theorem in abstract harmonic analysis, Matematicko-Fyzikalny Casopis 15 (1965), 43–48.Google Scholar
5.Lee, A. J., Sampling theorems for nonstationary stochastic processes, Trans. Amer. Math. Soc. 242 (1978), 225–241.CrossRefGoogle Scholar
6.Lloyd, S. P., A sampling theorem for stationary (wide sense) stochastic processes, Trans. Amer. Math. Soc. 92 (1959), 1–12.Google Scholar
7.Loomis, L. H., An Introduction to Abstract Harmonic Analysis (Van Nostrand, New York, 1953).Google Scholar
8.Montgomery, D. and Zippin, L., Topological Transformation Groups (Interscience, New York, 1955).Google Scholar
9.Petersen, D. P., and Middleton, D., Sampling and reconstruction of wave-number-limited functions in N-dimensional Euclidean spaces, Inform, and Control 5 (1962), 279–323.CrossRefGoogle Scholar
10.Reza, F. M., An Introduction to Information Theory (McGraw-Hill, New York, 1961).Google Scholar
11.Rudin, W., Fourier Analysis on Groups (Interscience, New York, 1962).Google Scholar
12.Whittaker, E. T., On the functions which are represented by the expansions of the interpolation theory, Proc. Roy. Soc. Edinburgh 35 (1915), 181–194.CrossRefGoogle Scholar