No CrossRef data available.
Article contents
Note on the theory of the rolling of one rigid surface on another
Published online by Cambridge University Press: 20 January 2009
Extract
Take first the case of a surface S rolling on a plane, the instantaneous axis of rotation being a line in the tangent plane at the point of contact. Take that line as x-axis, and the normal as z-axis, and let the equation to the surface be
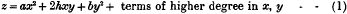
Then if p is small, the equation of the section of the surface S by the plane z = p is
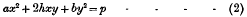
Now for rolling of this sort it is clear that the successive axes of rotation during a short time will be generators parallel to OX of a cylindrical surface which will touch S in the neighbourhood of O.
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1901


