Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:30:34.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the Integral Equations for the Lamé Functions

Published online by Cambridge University Press:  20 January 2009

E. T. Copson
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

§1. The Lamé Functions of degree n (where n is a positive integer) may be defined as those solutions of the equation

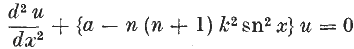
which are polynomials in the elliptic functions sn x, cn x, dn x of real modulus K. Such solutions only exist for certain particular values of the constant a; there are 2n + 1 such values and 2n + 1 corresponding Lamé functions.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 1 , Issue 1 , May 1927 , pp. 62 - 64
Copyright
Copyright © Edinburgh Mathematical Society 1927

References

page 62 note 1 Proc. Land. Math. Soc. (2) 14 (1915) 260.Google Scholar

Proc. B. S. Edin. 35 (1914–1915) 70.Google Scholar

See also Whittaker, and Watson, , Modern Analysis (3rd Edition, 1920), Ch. XXIII.Google Scholar

page 63 note 1 CfHeine, , Theorie der Kugelfunctionen, (1878), 355.Google Scholar

page 64 note 1 Proc. Lond. Math. Soc. (2) 20 (1921), 374.Google Scholar

page 64 note 2 Journ. of Dept. of Sc., Calcutta University 111 (1922). (Unfortunately I have been unable to verify this reference, as the journal is not in any of the Edinburgh libraries.)Google Scholar