No CrossRef data available.
Article contents
Note on the Elementary Divisors of Some Related Determinants
Published online by Cambridge University Press: 20 January 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The matrices considered in the following note are non-singular, and are related to a given matrix A having elements taken from the field of positive and negative integers and zero. The invariant properties of such a matrix A, under multiplications by matrices of determinant equal to unity, can be formulated, as is well known, in terms of the “elementary divisors” of the determinant |A|. Thus if A is of the nth order, and p is a prime occurring in |A| to the power hn, in the H.C.F. of the first minors of |A| to the power hn−1, in the H.C.F. of the second minors to the power hn−2, and so on, h0 by convention being zero, then the first differences of the h's,
are invariant under the transformations considered, and it is known that r ≥ er−1. The numbers
where the product includes all prime factors of |A|, are called the elementary divisors of |A| and
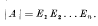
- Type
- Research Article
- Information
- Copyright
- Copyright © Edinburgh Mathematical Society 1928
References
page 166 note 1 See Muir, , History of the Theory of Determinant, vol. IV, chap. XXI, p. 439 on Smith, H. J. S.).Google Scholar
page 167 note 1 On the Latent Roots of Certain Matrices. Proc. Edin. Math. Hoc, Ser. 2, Vol. I, p. 135.Google Scholar
You have
Access