Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T06:23:04.451Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Capelli Operators associated with a Symmetric Matrix

Published online by Cambridge University Press:  20 January 2009

Andrew H. Wallace
Andrew H. Wallace
Affiliation:
University College, Dundee, (University of St. Andrews).
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the Proceedings of the Edinburgh Mathematical Society, 1948, there appear two papers by Lars Gårding and Turnbull respectively (Gårding [1], Turnbull [2]) which formulate the theory of Cayley and Capelli operators associated with symmetric matrices. Turnbull derives the modification, appropriate to symmetric matrices, of Capelli's Theorem, which states that (taking a third order operator for the sake of ease in writing)

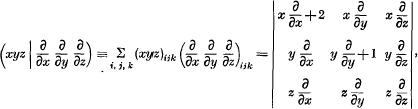
where the symbol (xyz)ijk stands for the determinant

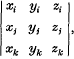
with a similar meaning for the determinantal differential operator, while the symbols are polarisations (Capelli [1]; cf. Turnbull [1], p. 116). Gårding's theorem deals with the effect of such modified Capelli operators on powers of the determinant of the symmetric matrix in question. The subject of this note is an alternative derivation of the modified Capelli theorem and of Gårding's theorem.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 9 , Issue 1 , October 1953 , pp. 7 - 12
Copyright
Copyright © Edinburgh Mathematical Society 1953

References

REFERENCES

Capelli, [1]: “Über die Zurūckführung des Cayleyschen Operatoren Ω auf gewöhnliche Polaroperatoren”, Math. Ann., 29 (1887), 331–338.Google Scholar
Gårdîng, [1]: “Extension of a Formula by Cayley to Symmetric Determinants”, Proc. Edinburgh Math. Soc. (2), 8 (1948), 73–75.CrossRefGoogle Scholar
Turnbull, [1]: Theory of Determinants, Matrices and Invariants (Second Edition, 1945).Google Scholar
Turnbull, [2]: “Symmetric Determinants and the Cayley and Capelli Operators”, Proc. Edinburgh Math. Soc. (2), 8 (1948), 76–86.Google Scholar
Weyl, [1]: The Classical Groups (Princeton, 1939).Google Scholar